A long horizontal rod has a bead which can slide along its length and initially placed at a 
distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping is
√μα
μ√α
1√μα
Infinitesimal
The correct Answer is:A
Tangential force (Ft) of the bead will be given by the normal reaction (N), while centripetal force (FC) is provided by friction (fr). The bead starts sliding when the centripetal force is just equal to the limiting friction. Therefore
Ft=ma=mαL=N
∴ limiting value of friction
(fr)_("max") = muN = mu m alpha L ..... (1)
Angular velocity at time t is ω:=αt
∴ Centripetal force at time t will be
Fc=mLω2=mLα2t2 .......... (2)
Equating equations (1) and (2), we get
t=√μα
For t>√μα,Fc>(fr)max
İ.e. the bead starts sliding. In the figure Ft is perpendicular to the paper inwards ⊗ .
Topper's Solved these Questions
Similar Questions
A conductor (rod) of mass m, length l carrying a current i is subjected to a magnetic field of induction B. If the coefficients of friction between the conducting rod and rail is μ, find the value of I if the rod starts sliding.
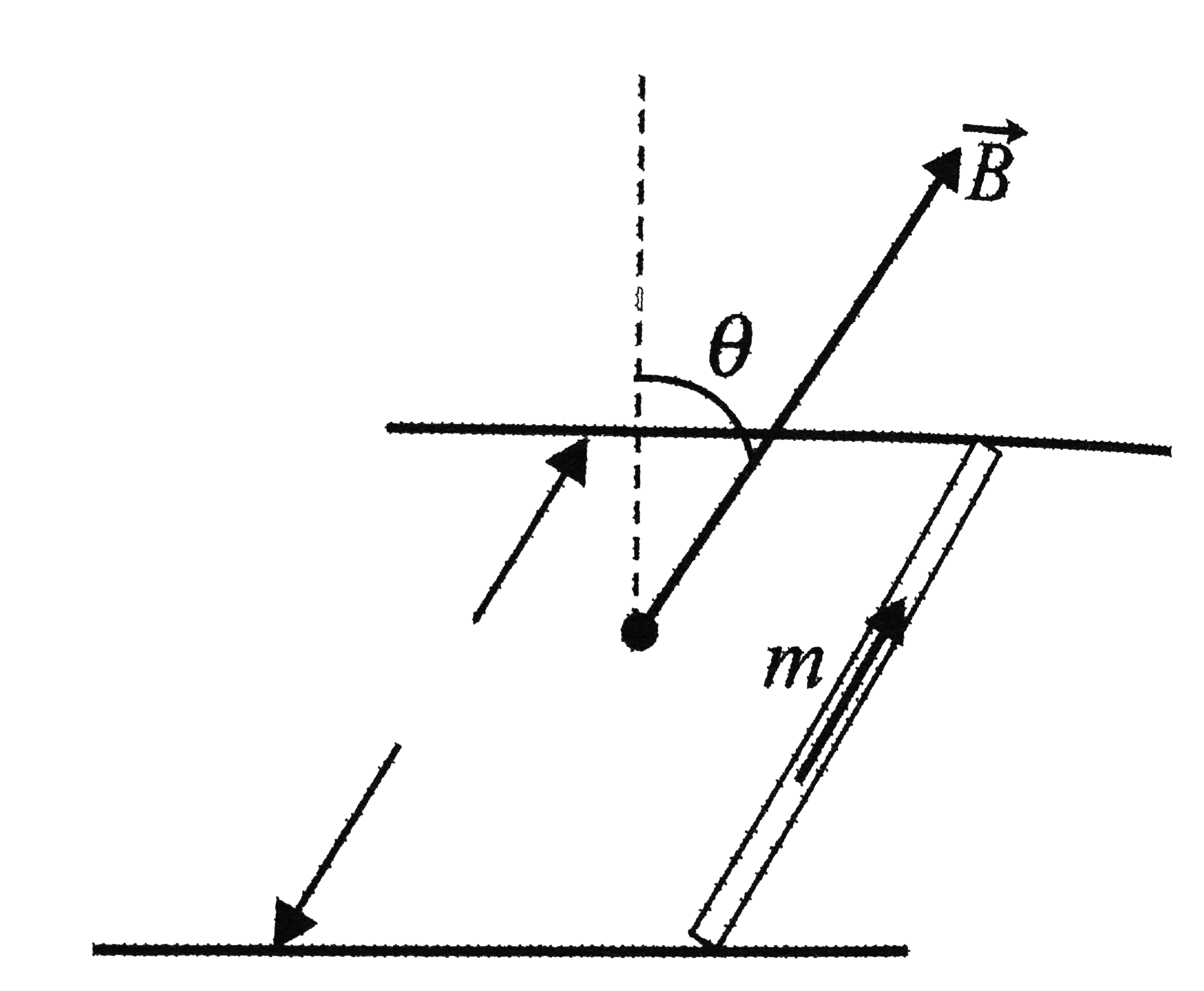View SolutionA uniform rod of length 2a is placed horizontally on the edge of a table. Initially the centre of mass of the rod is at a distance a/3 from the edge. The rod is released from rest. If the rod slips after it turned an angle θ, find the coefficient of friction between the rod and the table.
View Solution
Knowledge Check
A long horizontal rod has a bead which can slide along its length and initially placed at a
distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping isA√μαBμ√αC1√μαDInfinitesimalA long horizontal rod has a bead which can slide along its length and is initially placed at a distance L from one end A of the rod. The rod is set in angular motion about A with a constant angular acceleration, α. If the coefficient of friction between the rod and bead is μ, and gravity is neglected, then the time after which the bead starts slipping is :
A√μαBμ√αC1√μαDinfinitesimalA long horizontal rod has a bead which can slide along its length and initially placed at a
distance L from one end A of the rod. The rod is set in angular motion about A with constant angular acceleration α. if the coefficient of friction between the rod and the bead is μ, and gravity is neglected, then the time after which the bead starts slipping isA
B
C
D
L shaped rod whose one end is horizontal and other is vertical is rotating about a vertical axis as shown with angular speed ω .The sleeve has mass m and friction coefficient between rod and sleeve is μ.The minimum angular speed ω for which sleeve cannot slip on rod is?
View SolutionIn the arrangement shown in fig., mass of the rod M exceeds the mass m of the ball. The ball has an opening permitting it to slide along the thread with some friction. The mass of the pulley and the friction in its axle are negligible. At the initial moment, the ball was located opposite the lower end of the rod. When set free, both bodies began moving with constant accelerations. Find the friction force between the ball and the thread if t seconds after the beginning of motion, the ball got opposite to the upper end of the rod. The rod length equals l.
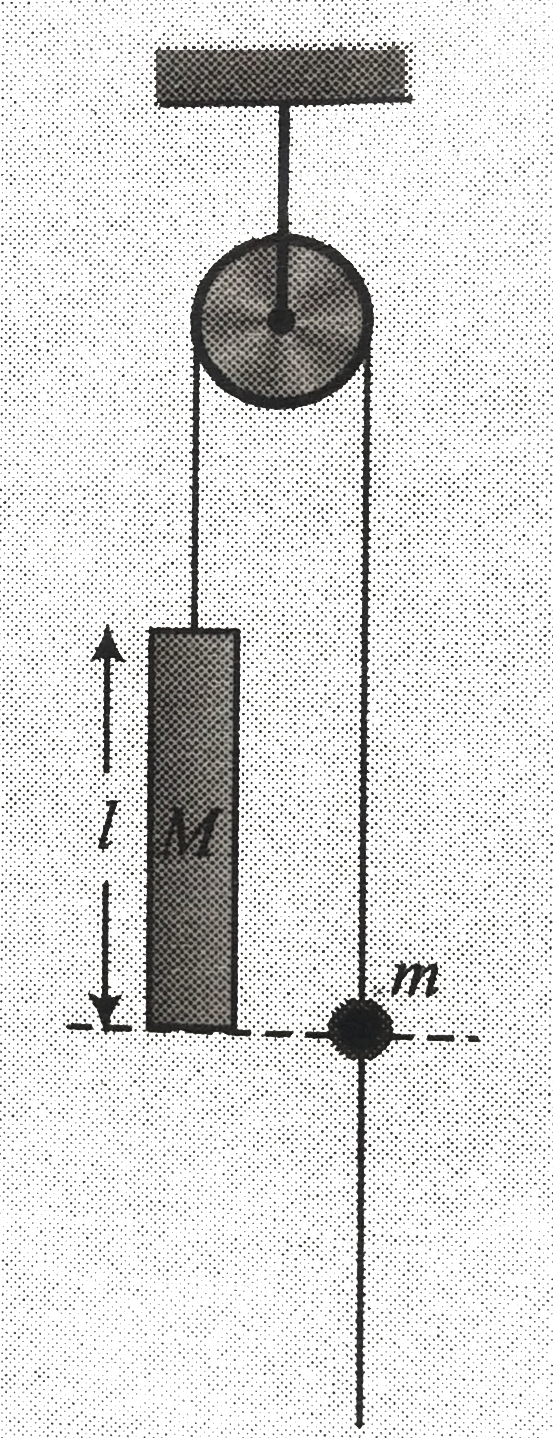View SolutionA rod is kept inclined at an angle θ with the horizontal A sleeve of mass m can slide on the rod. If the coefficient of friction between the rod and the sleeve is μ, for what values of horizontal acceleration a of the rod, towards left, the sleeve will not slide over the rod?
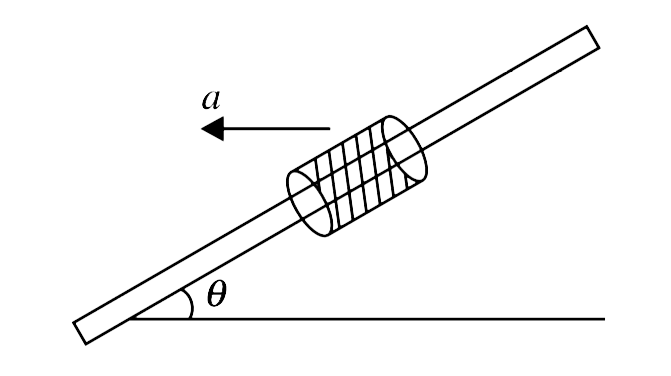View SolutionA rod can rotate in a horizontal plane about its one end. A bead which can move along the rod is placed at certain distance from the axis or rotation. The bead does not to friction. The rod has a constant angular acceleration
View SolutionA bead is contrained to move on rod in granvity free space as shown in figure. The rod rotating with ,angular velocity and angulnr acceleration α about its end. If μ is coefficient of friction. Mark the correct option. ( Rod rotates in the plane of paper.)
View Solution