In the arrangement shown in figure, coefficient of friction between two fixed points A & B which are at the same horizontal level. The inclination of the chain with the horizontal at both the points of support is θ. What is the tension of the chain at the mid point?

8 N
10 N
6 N
4 N
The correct Answer is:A
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JM)
Explore 6 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (JA)
Explore 4 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBook:ALLENChapter:NEWTON'S LAWS OF MOTION & FRICTIONExercise:EXERCISE (O-1)
Explore 51 Videos
- MOTION IN A PALNEBook:ALLENChapter:MOTION IN A PALNEExercise:SOLVED EXAMPLE
Explore 28 Videos
- NEWTONS LAWS OF MOTIONBook:ALLENChapter:NEWTONS LAWS OF MOTIONExercise:EXERCISE-III
Explore 28 Videos
Similar Questions
A flexible chain of weight W hangs between two fixed points A and B at the same level. The inclination of the chain with the horizontal at the two points of support is θ=60∘. What is the tension of the chain at the point P where inclination of chain with horizonrtal is ϕ=30∘

View SolutionA flexible chain of weight W hangs between two fixed points A and B at the same level. The inclination of the chain with the horizontal at the two points of support is θ. Calculated the tension of the chain at end points and also at the lower most point .
[Hints : Consider equilibrium of each half of the chain. ]
View Solution
Knowledge Check
A flexible chain of weight W hangs between two fixed points A & B which are at the same horizontal level. The inclination of the chain with the horizontal at both the points of support is θ . What is the tension of the chain at the mid point ?
 AW2cosecθBW2tanθCW2tanθDnone
AW2cosecθBW2tanθCW2tanθDnoneA flexible chain of weight W hangs between two fixed points A and B at the same level. The inclination of the chain with the horizontal at the two points of support is θ=60∘. What is the tension of the chain at the point P where inclination of chain with horizonrtal is ϕ=30∘
 A2W3BW2CWDW3
A2W3BW2CWDW3In the arrangement shown in figure, coefficient of friction between the two blocks is μ=1/2. The force of friction acting between
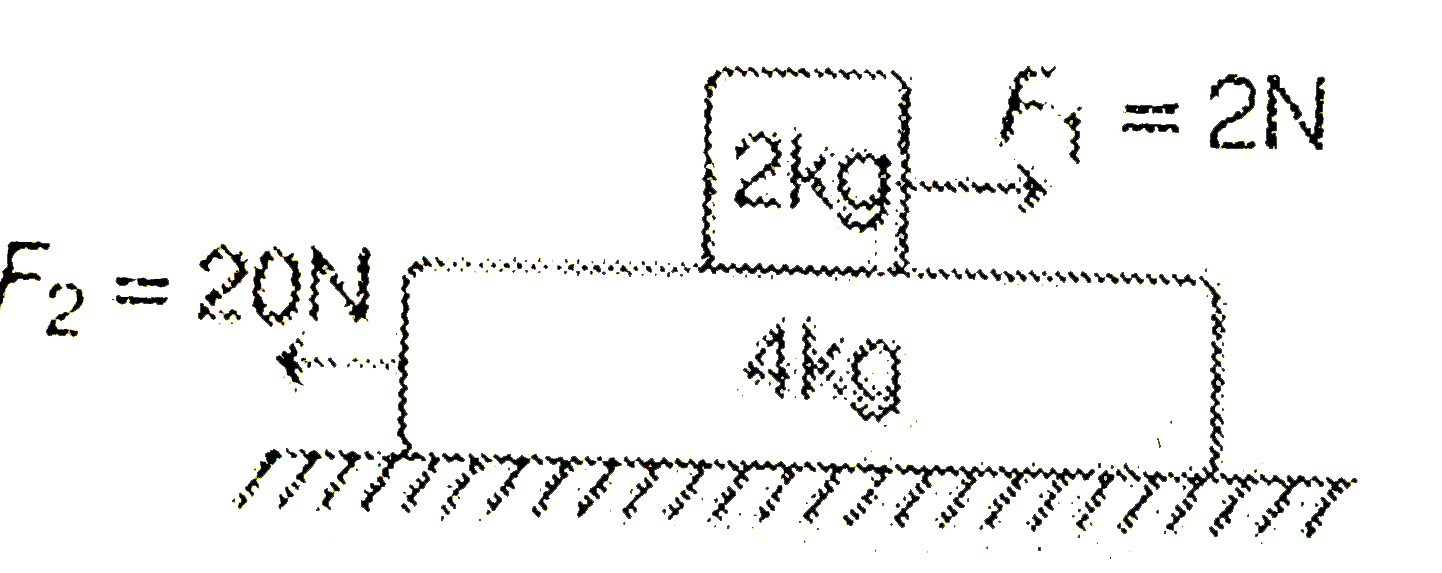 A8NB10NC6ND4N
A8NB10NC6ND4N
A flexible chain of weight W hangs between two fixed points A and B at the same level. The inclination of the chain with the horizontal at the two points of support is θ. Calculated the tension of the chain at end points and also at the lower most point .
[Hints : Consider equilibrium of each half of the chain. ]
View SolutionFor the arrangement shown in the figure the coefficient of friction between the two blocks is μ. If both the blocks are identical and moving ,then the acceleration of each block is

View SolutionDetermine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.
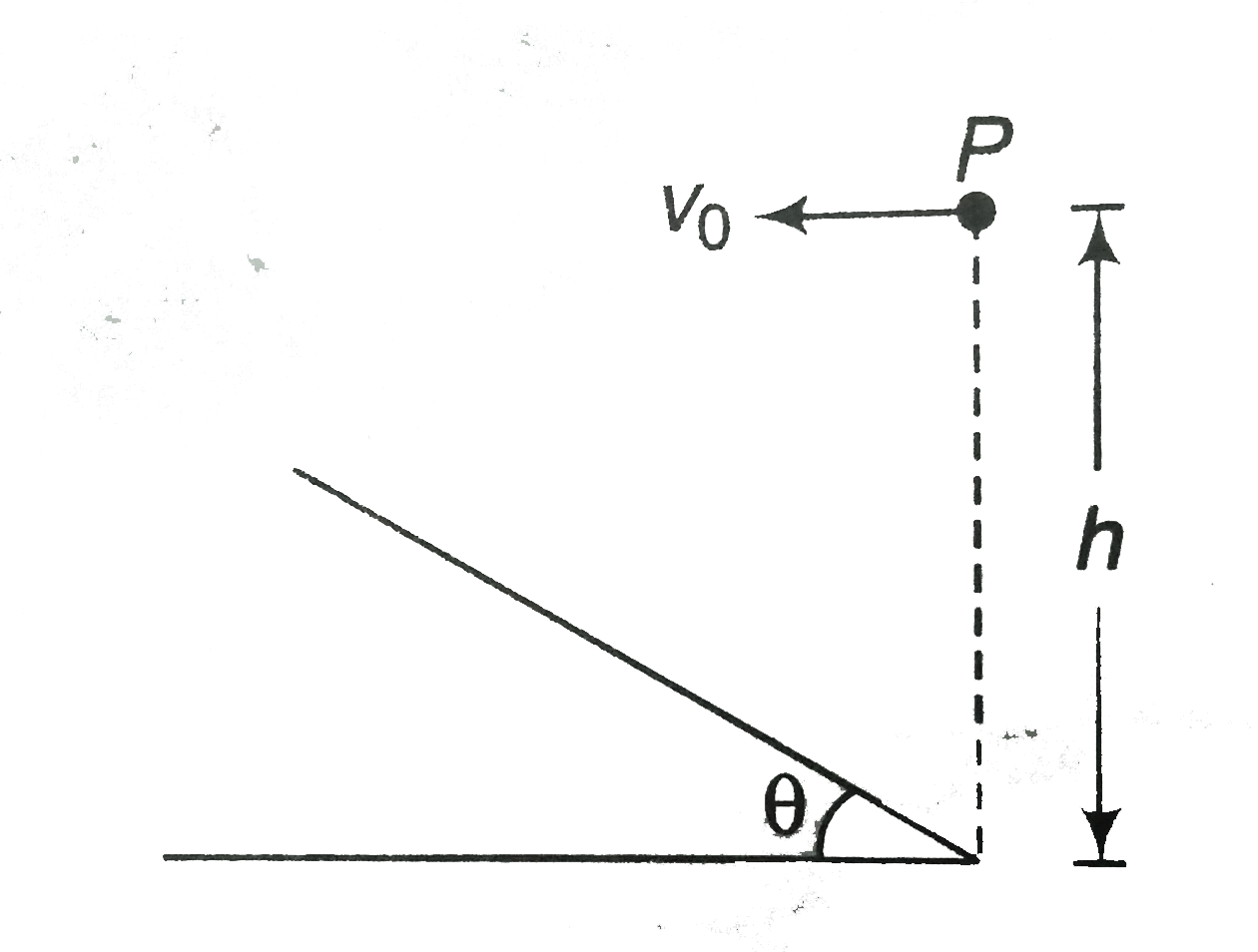
View SolutionDetermine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.

View SolutionFor the arrangement shown in the figure the coefficient of friction between the two blocks is μ. If both the blocks are identical and moving ,then the acceleration of each block is

View Solution
