A flexible chain of weight W hangs between two fixed points A and B at the same level. The inclination of the chain with the horizontal at the two points of support is θ. Calculated the tension of the chain at end points and also at the lower most point .
[Hints : Consider equilibrium of each half of the chain. ]
W2.cosecθ, zero
W2.tanθ , zero
zero ,W2cotθ
none
The correct Answer is:C
To solve the problem of a flexible chain of weight W hanging between two fixed points A and B at the same level, with an inclination θ at the points of support, we will analyze the forces acting on the chain.
1. Visualize the Setup:
- Draw the chain hanging between points A and B.
- The chain makes an angle θ with the horizontal at both ends.
2. Identify Forces:
- The weight W of the chain acts downwards at the midpoint (the lowest point) of the chain.
- At points A and B, the tension in the chain can be denoted as T.
3. Consider Equilibrium of Each Half of the Chain:
- For the left half of the chain (from A to the midpoint C):
- The vertical component of the tension must balance the weight of the chain.
- The vertical component of tension at point A is Tsinθ.
4. Balance Forces:
- The total vertical force due to the tension from both sides (left and right) at the midpoint C is:
2Tsinθ=W
- From this equation, we can solve for T:
T=W2sinθ
5. Tension at the End Points:
- The tension at points A and B is given by:
TA=TB=W2sinθ
6. Tension at the Lowermost Point C:
- At the lowest point C, the tension is affected by the forces from both sides.
- The horizontal components of tension from both sides cancel each other out, and since there are no vertical forces acting at point C (the weight W is balanced by the vertical components of tension), the net tension at point C is:
TC=0
Final Results:
- Tension at points A and B:
TA=TB=W2sinθ
- Tension at the lowermost point C:
TC=0
- Draw the chain hanging between points A and B.
- The chain makes an angle θ with the horizontal at both ends.
- The weight W of the chain acts downwards at the midpoint (the lowest point) of the chain.
- At points A and B, the tension in the chain can be denoted as T.
- For the left half of the chain (from A to the midpoint C):
- The vertical component of the tension must balance the weight of the chain.
- The vertical component of tension at point A is Tsinθ.
- The total vertical force due to the tension from both sides (left and right) at the midpoint C is:
2Tsinθ=W
- From this equation, we can solve for T:
T=W2sinθ
- The tension at points A and B is given by:
TA=TB=W2sinθ
- At the lowest point C, the tension is affected by the forces from both sides.
- The horizontal components of tension from both sides cancel each other out, and since there are no vertical forces acting at point C (the weight W is balanced by the vertical components of tension), the net tension at point C is:
TC=0
- Tension at points A and B:
TA=TB=W2sinθ
- Tension at the lowermost point C:
TC=0
Topper's Solved these Questions
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JM)
6 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (JA)
4 Videos
- NEWTON'S LAWS OF MOTION & FRICTIONBOOK - ALLENCHAPTER - NEWTON'S LAWS OF MOTION & FRICTIONEXERCISE - EXERCISE (O-1)
51 Videos
- MOTION IN A PALNEBOOK - ALLENCHAPTER - MOTION IN A PALNEEXERCISE - SOLVED EXAMPLE
28 Videos
- NEWTONS LAWS OF MOTIONBOOK - ALLENCHAPTER - NEWTONS LAWS OF MOTIONEXERCISE - EXERCISE-III
28 Videos
Similar Questions
A flexible chain of weight W hangs between two fixed points A and B at the same level. The inclination of the chain with the horizontal at the two points of support is θ=60∘. What is the tension of the chain at the point P where inclination of chain with horizonrtal is ϕ=30∘

View Solution
A block of mass m is suspended from one end of a light spring as shown. The origin O is considered at distance equal to natural length of the spring from the ceiling and vertical downwards direction as positive y-axis. When the system is in equilibrium a bullet of mass m3 moving in vertical up wards direction with velocity v0 strikes the block and embeds into it. As a result, the block (with bullet embedded into it) moves up and start oscillating. Based on the given information, answer the following question:
Q. The time taken by the block bullet system to move from y=mgk (initial equilibrium position) to y=0 (natural length of spring) is (A represents the amplitude of motion)
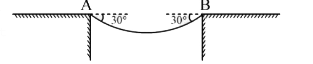
View SolutionA uniform cable has a mass of 100 kg and is suspended between two fixed points A and B, at the same horizontal level. At the support points the cable makes angles of as shown in figure. Choose the correct option. (g = 10 m/s2)
View SolutionA block of mass m is pulled by a uniform chain of mass m tied to it by applying a force F at the other end of the chain.The tension at a point P which is at a distance of quarter of the length of the chain from the free end,will be

View SolutionA heavy particle hanging from a fixed point by a light inextensible string of length l is projected horizontally with speed (gl) . Then the speed of the particle and the inclination of the string to the vertical at the instant of the motion when the tension in the string equal the weight of the particle-
View SolutionTwo particles are projected at the same instant from the same point at inclinations α and β to the horizontal. If they simultaneously hit the top and bottom of a vertical pole subtending angle θ at the point of projection , find (tanα−tanβ).
View SolutionTwo balls having masses m and 2m are fasrtened to two light strings of same length (figure). The other ends of the strings are fixed at O. The strings are kept in the same horizontal line and the system is released from rest. The collision between the balls is elastic. Point A is the lowest point at which either ball can reach
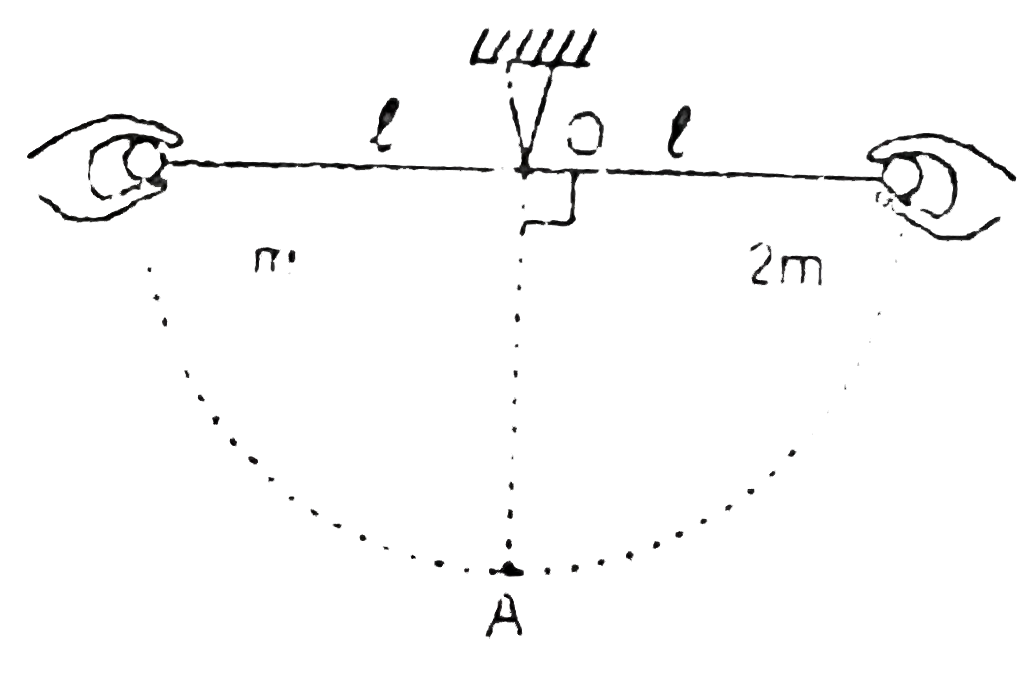
The position at which the balls will collide for the first time
View SolutionA unifrom flexible chain of length 32 m rests on a fixed smooth sphere of radius R=2π m such that one end A of chain is on the top of the sphere while the other end B is hanging freely. Chain is helpd stationary by a horizontal thread PA as shown . Calculate the acceleration of chain when the horizontal string PA is burnt ( g = 10 m/s2)
View SolutionA projectile passes two points A and B at same height after 2s and 6s of its projection. Horizontal separation between the points A and B is 120m. The horizontal range is closest to [g=10m/s2]

View SolutionA small stone of mass 100 g in rotated I a verticlal circle of radius 40 cm. What is the minimum speed needed at the lowest point for looping the loop? Also find the tension in the string at this point (g=10ms−2).
View Solution
