A satellite is orbiting around a planet. Its orbital velocity (V0) is found to depend upon
(A) Radius of orbit (R)
(B) Mass of planet (M)
(C ) Universal gravitatin contant (G)
Using dimensional anlaysis find and expression relating orbital velocity (V0) to the above physical quantities.
The correct Answer is:v0=k√GMR
To find an expression for the orbital velocity V0 of a satellite in terms of the radius of orbit R, the mass of the planet M, and the universal gravitational constant G, we will use dimensional analysis.
Step 1: Identify the dimensions of the quantities involved
1. Orbital Velocity V0: The dimension of velocity is given by:
(V0)=(L)(T−1)=LT−1
where L is length and T is time.
2. Radius of Orbit R: The dimension of radius is:
(R)=(L)
3. Mass of Planet M: The dimension of mass is:
(M)=(M)
4. Universal Gravitational Constant G: The dimension of G can be derived from the formula for gravitational force:
F=Gm1m2R2
Rearranging gives:
G=FR2m1m2
The dimension of force F is:
(F)=(M)(L)(T−2)=MLT−2
Thus, substituting into the equation for G:
(G)=MLT−2⋅L2M2=M−1L3T−2
Step 2: Formulate the relationship using dimensional analysis
Assume that the orbital velocity V0 can be expressed as a function of R, M, and G:
V0=kRaMbGc
where k is a dimensionless constant, and a, b, and c are the powers we need to determine.
Step 3: Write the dimensions of the right-hand side
Substituting the dimensions we found:
(V0)=(Ra)(Mb)(Gc)=(La)(Mb)(M−1L3T−2)c
This simplifies to:
(V0)=LaMbM−cL3cT−2c=La+3cMb−cT−2c
Step 4: Set up equations based on dimensions
Since both sides must be dimensionally equal, we can equate the powers of L, M, and T:
1. For L:
a+3c=1(1)
2. For M:
b−c=0(2)
3. For T:
−2c=−1(3)
Step 5: Solve the equations
From equation (3):
c=12
Substituting c into equation (2):
b−12=0⟹b=12
Substituting c into equation (1):
a+3×12=1⟹a+32=1⟹a=1−32=−12
Step 6: Write the final expression
Now substituting the values of a, b, and c back into the expression for V0:
V0=kR−12M12G12
This can be rewritten as:
V0=k√MG√R
Conclusion
Thus, the expression relating the orbital velocity V0 to the radius of orbit R, mass of the planet M, and universal gravitational constant G is:
V0=k√MGR
(V0)=(L)(T−1)=LT−1
where L is length and T is time.
(R)=(L)
(M)=(M)
F=Gm1m2R2
Rearranging gives:
G=FR2m1m2
The dimension of force F is:
(F)=(M)(L)(T−2)=MLT−2
Thus, substituting into the equation for G:
(G)=MLT−2⋅L2M2=M−1L3T−2
V0=kRaMbGc
where k is a dimensionless constant, and a, b, and c are the powers we need to determine.
(V0)=(Ra)(Mb)(Gc)=(La)(Mb)(M−1L3T−2)c
This simplifies to:
(V0)=LaMbM−cL3cT−2c=La+3cMb−cT−2c
1. For L:
a+3c=1(1)
2. For M:
b−c=0(2)
3. For T:
−2c=−1(3)
c=12
b−12=0⟹b=12
a+3×12=1⟹a+32=1⟹a=1−32=−12
V0=kR−12M12G12
This can be rewritten as:
V0=k√MG√R
V0=k√MGR
Topper's Solved these Questions
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (S-2)7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (O-1) Single Correct Type Questions.37videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
- BOOK - ALLENCHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Solved Examples7videos
UNIT & DIMENSIONS, BASIC MATHS AND VECTOR
- BOOK - ALLENCHAPTER - TEST PAPERSEXERCISE - MATHS18videos
TEST PAPERS
- BOOK - ALLENCHAPTER - WAVE OPTICSEXERCISE - Exercise 2 (Previous Year Questions)7videos
WAVE OPTICS
Similar Questions
A planet moves around the sun in nearly circular orbit. Its period of revolution 'T' depends upon :
(i) radius 'r' or orbit (ii) mass 'M' of the sum and
(iii) the gravitational constant G.
Show dimensionally that T2∝r2.View SolutionConsider a planet of mass (m), revolving round the sun. The time period (T) of revolution of the planet depends upon the radius of the orbit (r), mass of the sun (M) and the gravitational constant (G). Using dimensional analysis, verify Kepler' third law of planetary motion.
View Solution
Knowledge Check
- Question 1 - Select One
A satellite of mass m s revolving in circlular orbit of radius r aroiund the earth its angular momentum w.r.t the centre of its orbit is (M=mass of earth G= universal gravitational constant )
A(GMmr)1/2B(GM2mr)1/2C(GMm2r2)1/2D(GM2m2r)1/2 - Question 2 - Select One
The graph that represents the relation between orbital velocity (v0) of a satellite and radius (r) of the orbit around earth is
A B
B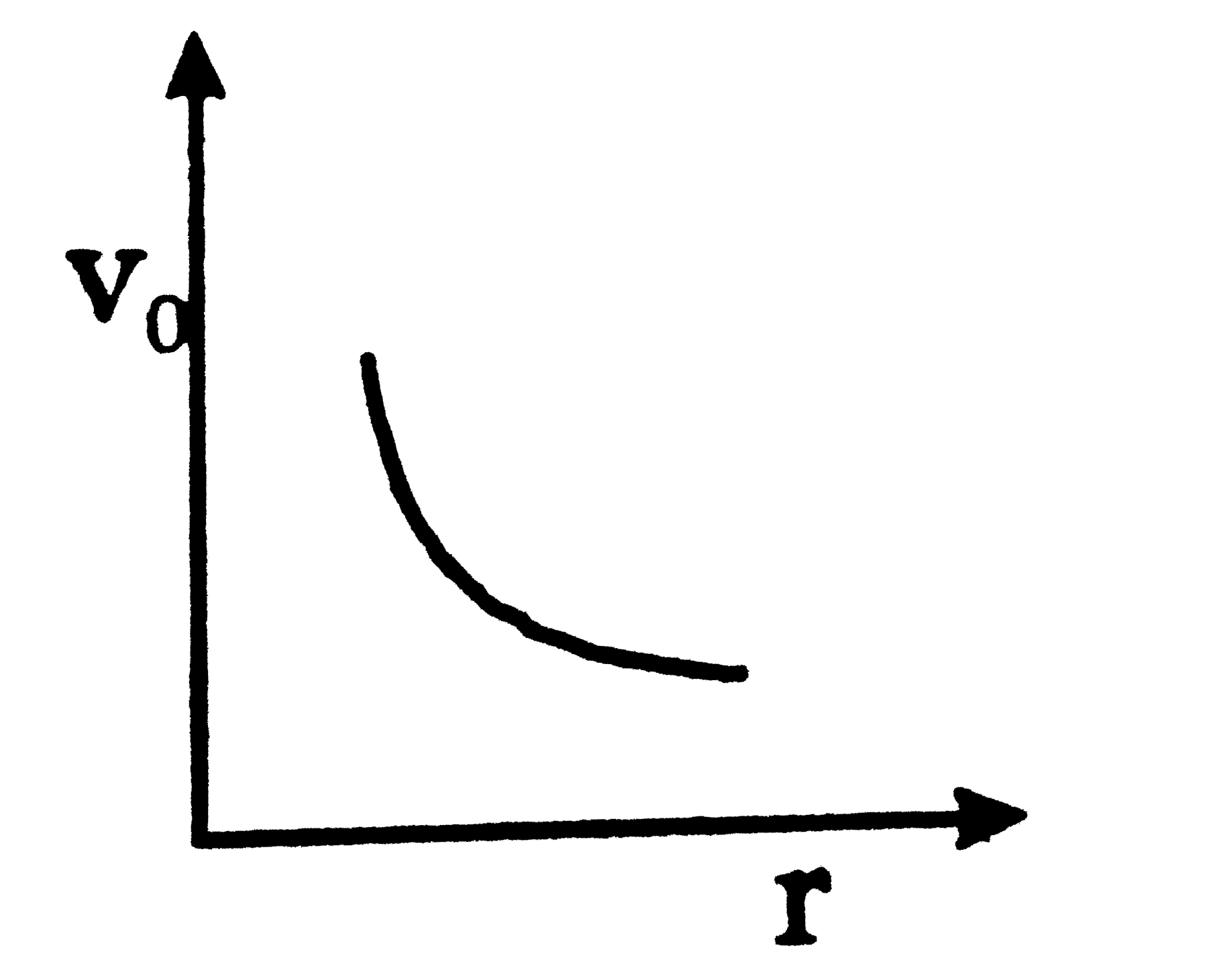 C
C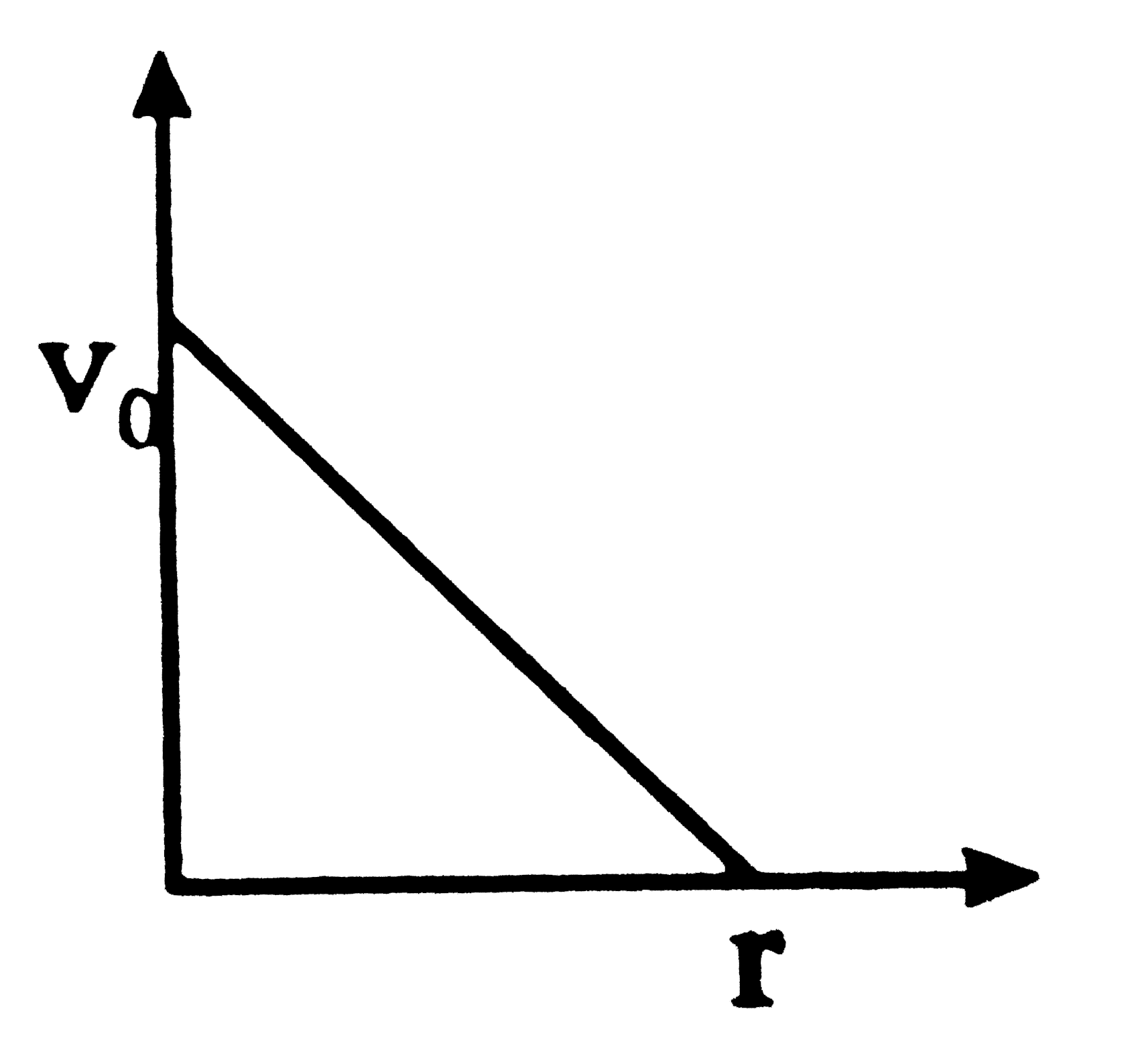 D
D
- Question 3 - Select One
The satellite of mass m is orbiting around the earth in a circular orbit with a velocity v.What will be its total energy ?
A(3/4)mv2B(1/2)mv2Cmv2D(1/2)mv2
Define orbital velocity. Derive an expression for the orbital velocity of a satellite revolving around a planet
View SolutionA satellite revolves close to the surface of a planet. How is its orbital velocity related with escape velocity of that planet.
View SolutionThe period of revolution(T) of a planet moving round the sun in a circular orbit depends upon the radius (r) of the orbit, mass (M) of the sun and the gravitation constant (G). Then T is proportioni of ra. The value of a is
View SolutionA satellite is orbiting with areal velocity va. At what height form the surface of the earth, it is rotating, if the radius of earth is R?
View SolutionHow many times is escape velocity (Ve) , of orbital velocity (V0) for a satellite revolving near earth
View Solution

