If three wires of equal resistance are given then number of combination they cany be made to give different resistance is
4
3
5
2
The correct Answer is:A
To solve the question of how many different combinations of three wires of equal resistance can be made to give different resistances, we can follow these steps:
Step 1: Understand the configurations
We can connect resistors in two basic configurations: series and parallel. We will explore all possible combinations of these configurations using three resistors.
Step 2: Series Connection
When all three resistors (let's denote the resistance of each wire as R) are connected in series, the total resistance Rs is given by:
Rs=R+R+R=3R
This is our first combination.
Step 3: Parallel Connection
When all three resistors are connected in parallel, the total resistance Rp is given by:
1Rp=1R+1R+1R=3R⟹Rp=R3
This is our second combination.
Step 4: Two in Parallel, One in Series
Now, let's connect two resistors in parallel and the third resistor in series with this combination. The equivalent resistance of the two resistors in parallel is:
1Rparallel=1R+1R=2R⟹Rparallel=R2
Now, adding the third resistor in series gives:
Rtotal=Rparallel+R=R2+R=3R2
This is our third combination.
Step 5: Two in Series, One in Parallel
Next, we can connect two resistors in series and then connect this combination in parallel with the third resistor. The equivalent resistance of the two resistors in series is:
Rseries=R+R=2R
Now, connecting this in parallel with the third resistor gives:
1Rtotal=12R+1R=1+22R=32R⟹Rtotal=2R3
This is our fourth combination.
Step 6: Count the Combinations
We have found four distinct combinations of resistances:
1. 3R (all in series)
2. R3 (all in parallel)
3. 3R2 (two in parallel, one in series)
4. 2R3 (two in series, one in parallel)
Conclusion
Thus, the total number of different combinations of three wires of equal resistance that can be made is 4.
We can connect resistors in two basic configurations: series and parallel. We will explore all possible combinations of these configurations using three resistors.
When all three resistors (let's denote the resistance of each wire as R) are connected in series, the total resistance Rs is given by:
Rs=R+R+R=3R
This is our first combination.
When all three resistors are connected in parallel, the total resistance Rp is given by:
1Rp=1R+1R+1R=3R⟹Rp=R3
This is our second combination.
Now, let's connect two resistors in parallel and the third resistor in series with this combination. The equivalent resistance of the two resistors in parallel is:
1Rparallel=1R+1R=2R⟹Rparallel=R2
Now, adding the third resistor in series gives:
Rtotal=Rparallel+R=R2+R=3R2
This is our third combination.
Next, we can connect two resistors in series and then connect this combination in parallel with the third resistor. The equivalent resistance of the two resistors in series is:
Rseries=R+R=2R
Now, connecting this in parallel with the third resistor gives:
1Rtotal=12R+1R=1+22R=32R⟹Rtotal=2R3
This is our fourth combination.
We have found four distinct combinations of resistances:
1. 3R (all in series)
2. R3 (all in parallel)
3. 3R2 (two in parallel, one in series)
4. 2R3 (two in series, one in parallel)
Thus, the total number of different combinations of three wires of equal resistance that can be made is 4.
Similar Questions
What is the ratio of equivalent resistance of series combination of n equal resistance to the equivalent resistance in parallel combination of these n resistances ?
View SolutionGiven three resistors of resistances 1Ω,2Ωand3Ω. How will you combine them to get an equivalent resistance of 115Ω ?
View Solution
Knowledge Check
- Question 1 - Select One
When three wires of unequal resistances are given the number of combinations they can be made to give different resistances is
A6B4C2D8 - Question 2 - Select One
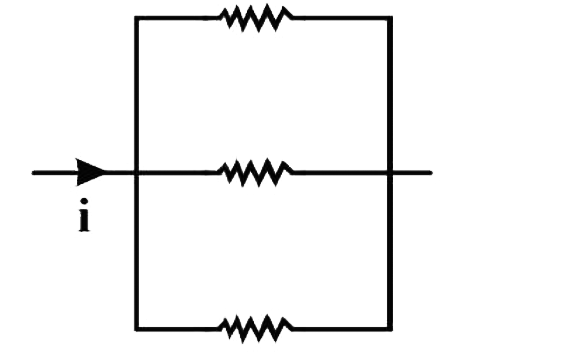
The three resistance of equal value are arranged in the different combination shown below. Arrange them in increasing order of power dissipation.
(I)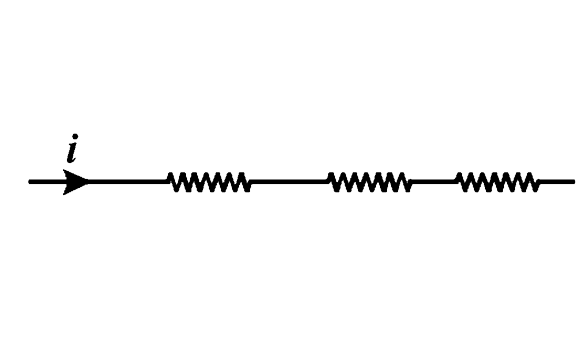 (II)
(II) 
 (IV)
(IV) 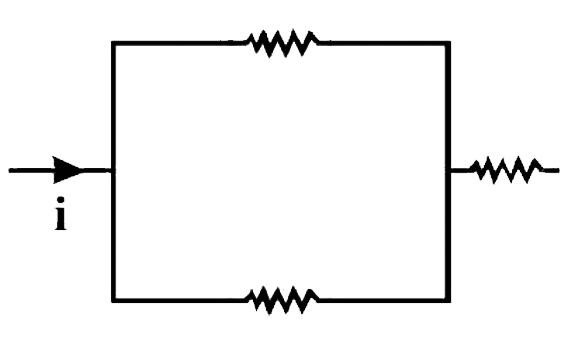 AIII<II<IV<IBII<III<IV<ICI<IV<III<IIDI<III<II<IV
AIII<II<IV<IBII<III<IV<ICI<IV<III<IIDI<III<II<IV - Question 3 - Select One

The three resistances of equal value are arranged in the different combinations shown below. Arrange them in increasing order of power dissipationAII<I<IIIBI>III>IICI<III<IIDI<II<III
Derive expression for equivalent resistance of a parallel combination of resistances.
(b) Calculate the ratio of equivalent resistance for a series combination of n number of identical resistors to the parallel combination of the same type of n number of resistors.View SolutionThe three resistances of equal values are arranged in the different combination shown in the figure. Arrange them in the increasing order of dissipation of power.
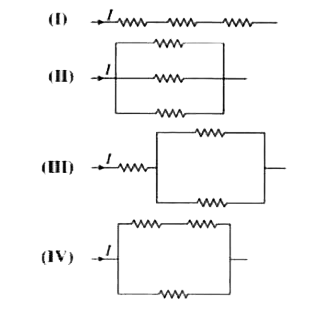 View Solution
View SolutionThe effective resistance of two wires is 2 x. The resistance of one wire is two times of the other wire and is three times the effective resistance. Which one of the following is correct in respet of value of x ?
View SolutionUsing three wires of resistances 1 ohm, 2 ohm and 3 ohm, then no.of different values of resistances that possible are
View SolutionUsing three wires of resistances 1 ohm, 2ohm and 3 ohm then no. of different values of resistances that possible are
View Solution

