Considering the earth as a short magnet with its centre coinciding with the centre of earth, show that the angle of dip ϕ is related to magnetic latitude λ through the relation tanϕ=2tanλ
Considering the situation for dipole, at position (r,θ) we have
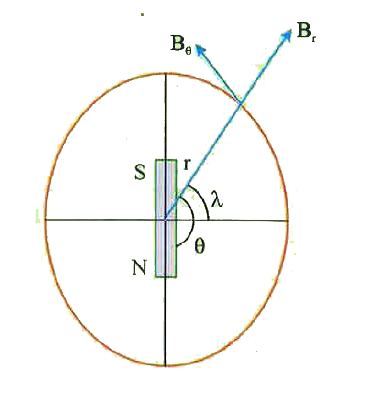
Br=μ04π2Mcosθr3andBθ=μ04πMsinθr3
and as tanϕ=BVBH=−BrBθ, so in the light of Eq. (1)
tanϕ=−2cotθ, But From figure θ=90∘+λ
So, tanϕ=−2cot(90∘+λ),i.e.,tanϕ=2tanλ
Topper's Solved these Questions
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - C.U.Q
87 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 1 (C.W)
52 Videos
- MAGNETISMBOOK - NARAYNACHAPTER - MAGNETISMEXERCISE - LEVEL-II (H.W)
24 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 4
20 Videos
Similar Questions
Considering the earth's magnetism to be due to a very powerful short magnet embedded at its centre placed with its south pole pointing north, show that, latutde (λ) of any place bears a definite relation with the dip (δ) of the place and that definite relation is tanδ=2tanλ
View SolutionA short bar magnet placed in a horizontal plane has its axis aligned along the magnetic north south direction. Null points are found on the axis of the magnet at 14cm from the centre of the magnet. The earth's magnetic field at the plane is 0⋅36G and the angle of dip is zero. What is the total magnetic field on the normal bisector of the magnet at the same distance as the null points (i.e. 14 cm) from the centre of the magnet? (At null points, field due to a magnet is equal and apposite to the horizontal component of earth's magnetic field).
View Solution
Knowledge Check
Angle of dip δ and latitude λ on earth's surface are related as
Atanδ=2tanλBtanδ=cotλCtanδ=tanλ2Dtanδ=tanλThe earth's magnetic field may be considered to be due to a short magnet placed at the centre of the earth annd oriented along the magnetic south-north direction. The ratio of the magnitude of the magnetic field on the earth's magnetic equator to that at the magnetic poles is
A1:2B2:1C1:4D4:1Let the magnetic field on earth be modelled by that of a point magnetic dipole at the centre of earth. The angle of dip at a point on the geographical equator
Ais always zeroBcan be zero at specific pointsCcan be positive or negativeDis bounded
Two coils each of 100 turns are held such that one lies in vertical plane and the other in the horizontal plane with their centres coinciding. The radius of the vetical coil is 0.20m and that of the horizontal coil is 0.30m. How will you neutralize the magnetic field of the earth at their common centre? What is the current to be passed through each coil? Horizontal component of earth's magnetic field =0.35×10−4T and angle of dip =30∘.
View SolutionA short bar magnet placed in a horizontal plane has its axis aligned along the magnetic north south direction. Null points are found on the axis of the magnet at 14 cm from the centre of the magnet. The earth's magnetic field at the place is 0.36 G and the angle of dip is zero. What is the total magnetic field on the normal bisector of the magnet at the same distance as the null point (i.e., 14 cm) from the centre of the magnet ? (At null points, field due to a magnet is equal and opposite to the horizontal component of earth's magnetic field.)
View SolutionLet the magnetic field on earth be modeled by that of a point magnetic dipole at the centre of earth. The angle of dip at a point on the geographical equator is
View SolutionAssertion : The magnetic Held lines of the earth resemble that of a magnetic dipole located at the centre of the earth.
Reason : The axis of the dipole coincide with the axis of rotation of the earth.
View SolutionWe can define two planes for a particular location on the surface of earth. One is called magnetic meridian and the other is called geographic meridian. Magnetic meridian for a point on the surface of earth is defined as a plane passing through this point and containing magnetic axis of earth. Similarly geographic meridian for a point on the surface of earth is defined as plane passing through this point and containing geographic axis of rotation. If we draw these two planes for a point on the surface of earth then in general these are found at some angle. Angle between these two planes is called declination for that place. Importance of magnetic meridian at a point is that net magnetic field vector of earth for that point lies on this plane. Usually net magnetic field of earth is inclined at some angle with the horizontal and this angle is called angle of dip for that place.
Which of the following planes pass through the centre of earth?
View Solution
