Relation between μrandχ will be
μr=1+χ
χ=μr+1
μ0μ
μ0χ
The correct Answer is:A
To find the relation between relative permeability (μr) and magnetic susceptibility (χ), we can follow these steps:
1. Understand the Definitions:
- Relative permeability (μr) is defined as the ratio of the permeability of a material (μ) to the permeability of free space (μ0):
μr=μμ0
- Magnetic susceptibility (χ) is a measure of how much a material will become magnetized in an applied magnetic field.
2. Use the Relation of Permeability:
- The permeability (μ) of a material can be expressed in terms of the permeability of free space and the magnetic susceptibility:
μ=μ0(1+χ)
3. Substituting into the Relative Permeability Formula:
- Substitute the expression for μ into the relative permeability formula:
μr=μμ0=μ0(1+χ)μ0
4. Simplifying the Expression:
- The μ0 terms cancel out:
μr=1+χ
5. Final Relation:
- Thus, the relation between relative permeability and magnetic susceptibility is:
μr=1+χ
Conclusion:
The final relation between relative permeability (μr) and magnetic susceptibility (χ) is:
μr=1+χ
- Relative permeability (μr) is defined as the ratio of the permeability of a material (μ) to the permeability of free space (μ0):
μr=μμ0
- Magnetic susceptibility (χ) is a measure of how much a material will become magnetized in an applied magnetic field.
- The permeability (μ) of a material can be expressed in terms of the permeability of free space and the magnetic susceptibility:
μ=μ0(1+χ)
- Substitute the expression for μ into the relative permeability formula:
μr=μμ0=μ0(1+χ)μ0
- The μ0 terms cancel out:
μr=1+χ
- Thus, the relation between relative permeability and magnetic susceptibility is:
μr=1+χ
The final relation between relative permeability (μr) and magnetic susceptibility (χ) is:
μr=1+χ
Topper's Solved these Questions
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 4 (SINGLE ANSWER TYPE QUESTION)
17 Videos
- MAGNETISM AND MATTERBOOK - NARAYNACHAPTER - MAGNETISM AND MATTEREXERCISE - EXERCISE - 2 (H.W)
24 Videos
- MAGNETISMBOOK - NARAYNACHAPTER - MAGNETISMEXERCISE - LEVEL-II (H.W)
24 Videos
- MOVING CHARGES AND MAGNETISMBOOK - NARAYNACHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - EXERCISE - 4
20 Videos
Similar Questions
Knowledge Check
A convex lens made up of material of refractive index μ1, is immersed in a medium of refractive index μ2 as shown in the figure. The relation between μ1 and μ2 is
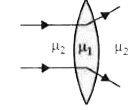 Aμ1<μ2Bμ1>μ2Cμ1=μ2Dμ1=√μ2
Aμ1<μ2Bμ1>μ2Cμ1=μ2Dμ1=√μ2The relation between radius (r) and diameter (d) is___
Ad=2xrBd=r/2Cd=r/3Dd=3rIn the following figure, the reading of an ideal voltmeter V is zero. Then, the relation between R, r1 and r2 is
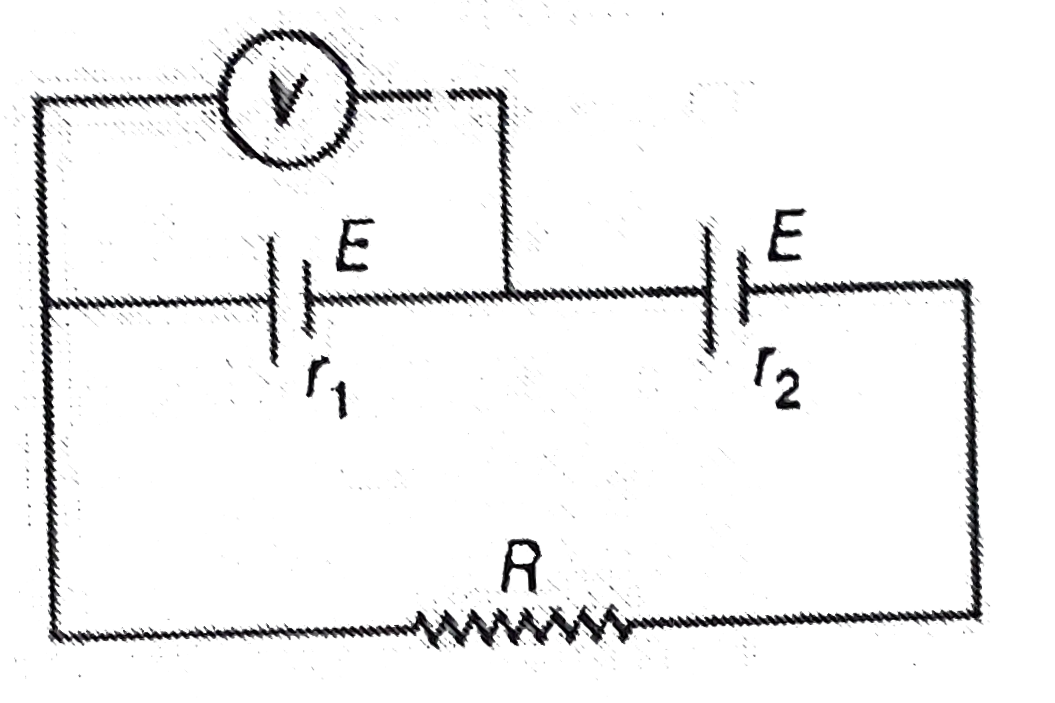 AR=r2−r1BR=r1−r2CR=r1+r2DR=r1r2r1+r2
AR=r2−r1BR=r1−r2CR=r1+r2DR=r1r2r1+r2
The relation between radius of third orbit r3 and radius of first orbit r1 in hydrogen atom would be
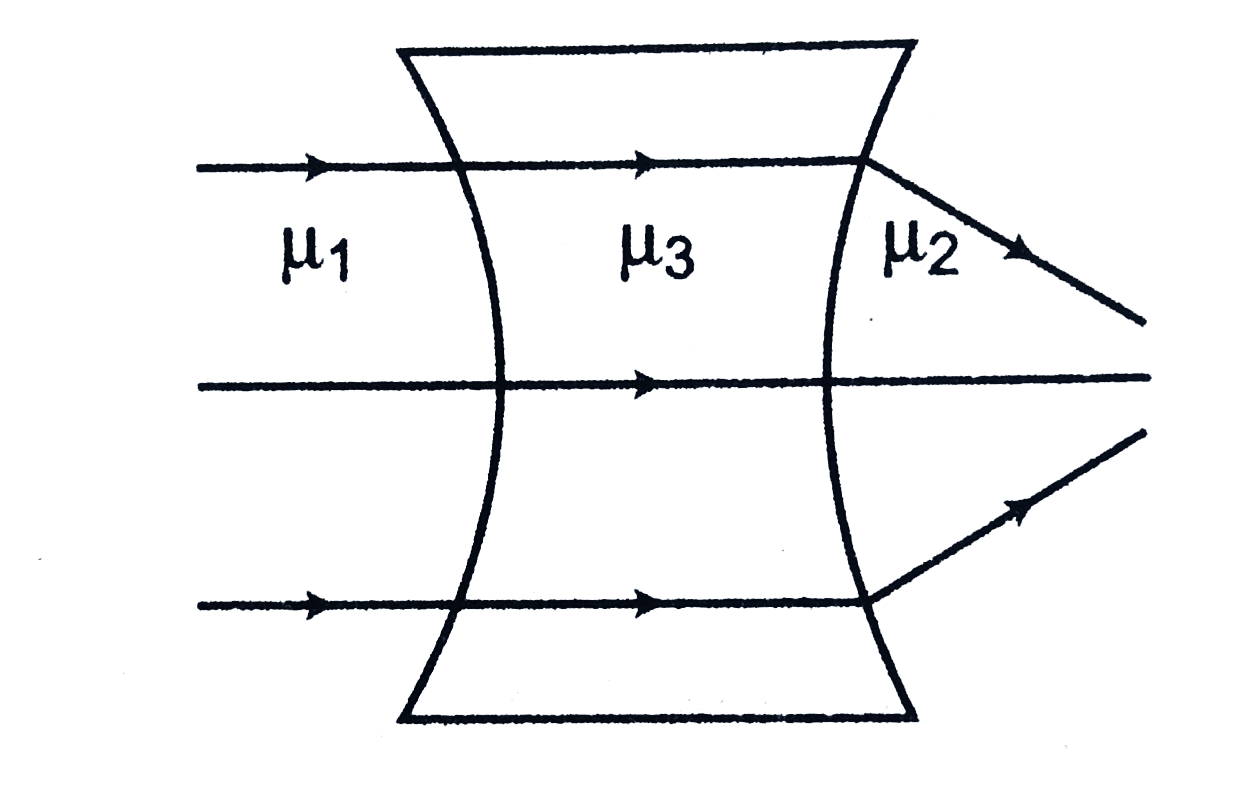
View SolutionFrom the figure shown, establish a relation between μ1,μ2,andμ3
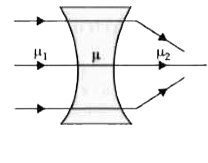
View SolutionIf the behaviour of light rays is as shown in the figure. The relation between refractive indices μ,μ1 "and" μ2 is
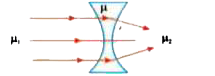
View SolutionThe relation between refractive indices u,μ1,μ2. if the behaviour of light ray is as shown in figure
View SolutionThe correct curve between refractive index μ and wavelength λ will be

View Solution