An a.c. voltage is applied to a pure inductor L, drives a current in the inductor. The current in the inductor would be
To solve the problem of finding the current in a pure inductor when an AC voltage is applied, we can follow these steps:
Step 1: Understand the Circuit
We have a pure inductor L connected to an AC voltage source. The voltage can be represented as:
V(t)=V0cos(ωt)
Step 2: Apply Kirchhoff's Law
According to Kirchhoff's law, the potential drop across the inductor VL is equal to the source voltage VS:
VL=VS
For an inductor, the voltage across it is given by:
VL=−Ldidt
Thus, we can write:
−Ldidt=V0cos(ωt)
Step 3: Rearrange the Equation
Rearranging the equation gives us:
didt=−V0Lcos(ωt)
Step 4: Integrate Both Sides
To find the current i(t), we need to integrate both sides. We can separate the variables:
di=−V0Lcos(ωt)dt
Integrating both sides gives:
∫di=−V0L∫cos(ωt)dt
The integral of cos(ωt) is:
∫cos(ωt)dt=1ωsin(ωt)+C
Thus, we have:
i=−V0Lωsin(ωt)+C
Step 5: Determine the Constant of Integration
Assuming the initial current i(0)=0 (the current starts from zero), we can find C:
0=−V0Lωsin(0)+C⟹C=0
Thus, the current becomes:
i(t)=−V0Lωsin(ωt)
Step 6: Express the Current in Terms of Cosine
Using the identity sin(ωt)=cos(ωt−π2), we can rewrite the current as:
i(t)=V0Lωcos(ωt−π2)
Conclusion
The final expression for the current in the inductor when an AC voltage is applied is:
i(t)=V0Lωcos(ωt−π2)
This indicates that the current lags the voltage by π2 radians (or 90 degrees).
We have a pure inductor L connected to an AC voltage source. The voltage can be represented as:
V(t)=V0cos(ωt)
According to Kirchhoff's law, the potential drop across the inductor VL is equal to the source voltage VS:
VL=VS
For an inductor, the voltage across it is given by:
VL=−Ldidt
Thus, we can write:
−Ldidt=V0cos(ωt)
Rearranging the equation gives us:
didt=−V0Lcos(ωt)
To find the current i(t), we need to integrate both sides. We can separate the variables:
di=−V0Lcos(ωt)dt
Integrating both sides gives:
∫di=−V0L∫cos(ωt)dt
The integral of cos(ωt) is:
∫cos(ωt)dt=1ωsin(ωt)+C
Thus, we have:
i=−V0Lωsin(ωt)+C
Assuming the initial current i(0)=0 (the current starts from zero), we can find C:
0=−V0Lωsin(0)+C⟹C=0
Thus, the current becomes:
i(t)=−V0Lωsin(ωt)
Using the identity sin(ωt)=cos(ωt−π2), we can rewrite the current as:
i(t)=V0Lωcos(ωt−π2)
The final expression for the current in the inductor when an AC voltage is applied is:
i(t)=V0Lωcos(ωt−π2)
This indicates that the current lags the voltage by π2 radians (or 90 degrees).
Similar Questions
Knowledge Check
An a.c. voltage is applied to a pure inductor L and drives a current in the inductor. The currentn in the inductor would be
Aahead of the voltage by π2Blagging the voltage by π2Cahead of the voltage by π4Dlagging the voltage by 3π4An AC voltage is applied to a resistance R and an inductor L in series . If R and the inductive reactance are both equal to 3 Ω, the phase difference between the applied voltage and the current in the circuit is
Aπ6Bπ4Cπ2Dzero.An a.c. Voltage is applied to a resistance R=30Ω and an inductor L in series. If the inductive reactance is also 30Ω, the phase difference between the applied voltage and the current in the circuit is
Aπ6Bπ2Cπ3Dπ4
Decay of current in inductor | Problems on inductor
View SolutionEnergy stored in an inductor is proportional to (i = current in the inductor)
View SolutionExplain the term 'inductive reactance'.Show graphically the variation of inductive reactance with frequency of the applied alternating voltage.
An a.c. voltage E=E0sinωt is applied across a pure inductor L.Show mathematically that the current flowing through it lags behind the applied voltage by a phase angle of π/2.
View SolutionThe frequency of oscillation of current in the inductor is:
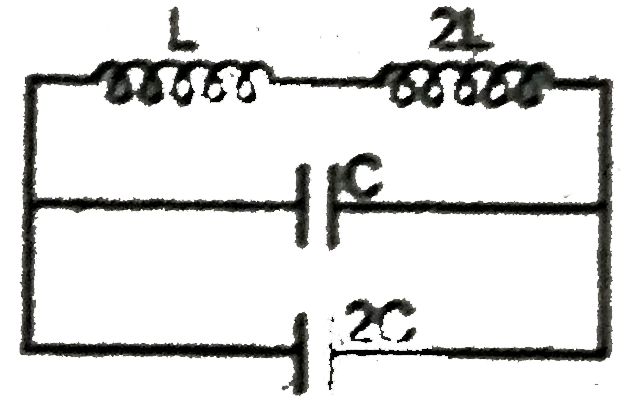
View SolutionThe frequency of oscillation of current in the inductor is-
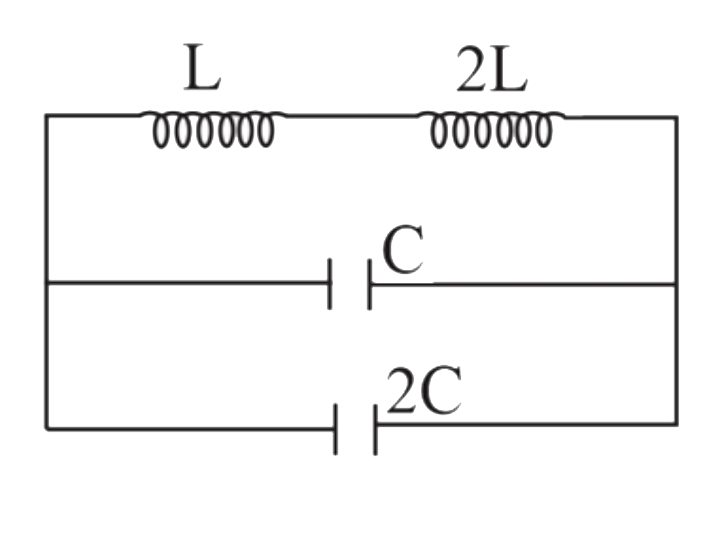
View Solution
