An a.c. voltage is applied to a pure inductor L, drives a current in the inductor. The current in the inductor would be
ahead voltage by π/2
lagging voltage by π/2
ahead voltage by 3π/2
lagging voltage by 3π/2
The correct Answer is:B
To solve the problem of the current in a pure inductor when an AC voltage is applied, we can follow these steps:
1. Understand the Setup:
We have a pure inductor (L) connected to an alternating current (AC) voltage source. The current flowing through the inductor will be sinusoidal due to the nature of AC voltage.
2. Express the Current:
The current (I) in the inductor can be expressed as:
I(t)=I0sin(ωt)
where I0 is the maximum current and ω is the angular frequency of the AC source.
3. Magnetic Flux in the Inductor:
The magnetic flux (Φ) linked with the inductor is given by:
Φ=L⋅I
Substituting the expression for current, we have:
Φ=L⋅I0sin(ωt)
4. Differentiate the Flux:
To find the induced electromotive force (EMF), we differentiate the magnetic flux with respect to time:
dΦdt=L⋅I0⋅ddt(sin(ωt))=L⋅I0⋅ωcos(ωt)
5. Relate EMF to Voltage:
The induced EMF (E) in the inductor is equal to the rate of change of magnetic flux:
E=−dΦdt=−L⋅I0⋅ωcos(ωt)
Since we are interested in the magnitude, we can write:
V=L⋅I0⋅ωcos(ωt)
6. Express Voltage in Sinusoidal Form:
The voltage can also be expressed in terms of sine:
V(t)=V0sin(ωt+π2)
where V0=L⋅I0⋅ω. The π2 phase shift indicates that the voltage leads the current.
7. Conclusion on Phase Relationship:
From the above expressions, we can conclude that:
- The current I(t)=I0sin(ωt)
- The voltage V(t)=V0sin(ωt+π2)
This shows that the current lags behind the voltage by π2 radians (or 90 degrees).
Final Answer:
The current in the inductor would be lagging the voltage by π2.
We have a pure inductor (L) connected to an alternating current (AC) voltage source. The current flowing through the inductor will be sinusoidal due to the nature of AC voltage.
The current (I) in the inductor can be expressed as:
I(t)=I0sin(ωt)
where I0 is the maximum current and ω is the angular frequency of the AC source.
The magnetic flux (Φ) linked with the inductor is given by:
Φ=L⋅I
Substituting the expression for current, we have:
Φ=L⋅I0sin(ωt)
To find the induced electromotive force (EMF), we differentiate the magnetic flux with respect to time:
dΦdt=L⋅I0⋅ddt(sin(ωt))=L⋅I0⋅ωcos(ωt)
The induced EMF (E) in the inductor is equal to the rate of change of magnetic flux:
E=−dΦdt=−L⋅I0⋅ωcos(ωt)
Since we are interested in the magnitude, we can write:
V=L⋅I0⋅ωcos(ωt)
The voltage can also be expressed in terms of sine:
V(t)=V0sin(ωt+π2)
where V0=L⋅I0⋅ω. The π2 phase shift indicates that the voltage leads the current.
From the above expressions, we can conclude that:
- The current I(t)=I0sin(ωt)
- The voltage V(t)=V0sin(ωt+π2)
The current in the inductor would be lagging the voltage by π2.
Similar Questions
Knowledge Check
An a.c. voltage is applied to a pure inductor L and drives a current in the inductor. The currentn in the inductor would be
Aahead of the voltage by π2Blagging the voltage by π2Cahead of the voltage by π4Dlagging the voltage by 3π4An AC voltage is applied to a resistance R and an inductor L in series . If R and the inductive reactance are both equal to 3 Ω, the phase difference between the applied voltage and the current in the circuit is
Aπ6Bπ4Cπ2Dzero.An a.c. Voltage is applied to a resistance R=30Ω and an inductor L in series. If the inductive reactance is also 30Ω, the phase difference between the applied voltage and the current in the circuit is
Aπ6Bπ2Cπ3Dπ4
Decay of current in inductor | Problems on inductor
View SolutionEnergy stored in an inductor is proportional to (i = current in the inductor)
View SolutionExplain the term 'inductive reactance'.Show graphically the variation of inductive reactance with frequency of the applied alternating voltage.
An a.c. voltage E=E0sinωt is applied across a pure inductor L.Show mathematically that the current flowing through it lags behind the applied voltage by a phase angle of π/2.
View SolutionThe frequency of oscillation of current in the inductor is-
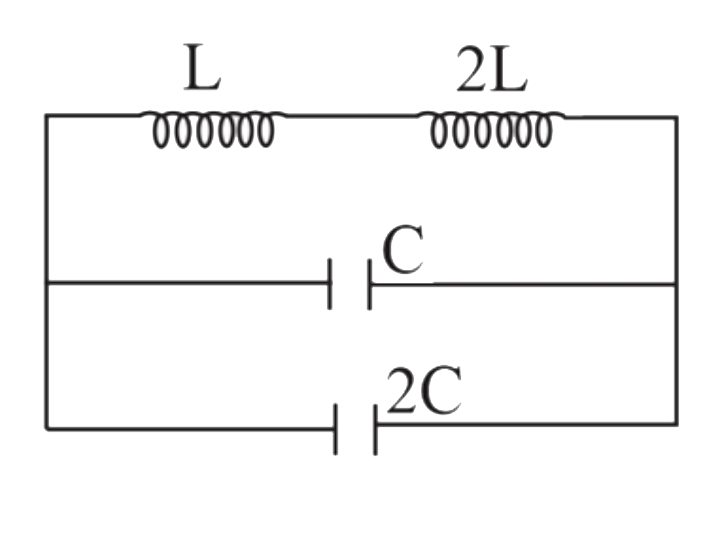
View SolutionThe frequency of oscillation of current in the inductor is:
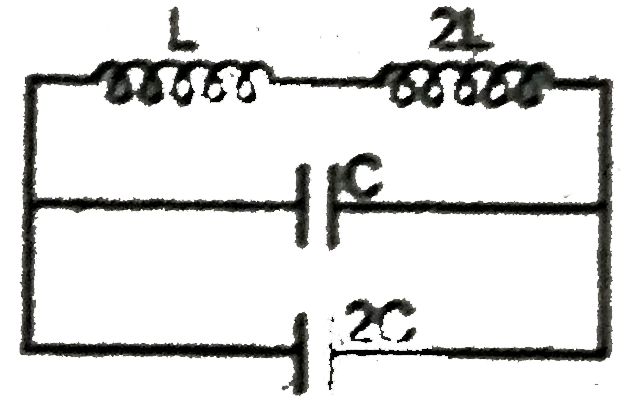
View Solution
