A ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

Deviation by a sphere is 2 (i - r)
Here, deviation δ=60∘=2(i−r) or i-r = 30∘
∴r=I−30∘=60∘−30∘=30∘
∴μ=sinisinr=sin60∘sin30∘=√3
Topper's Solved these Questions
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFLECTION)
9 Videos
- RAY OPTICS AND OPTICAL INSTRAUMENTS BOOK - NARAYNACHAPTER - RAY OPTICS AND OPTICAL INSTRAUMENTS EXERCISE - CUQ (REFRECTION)
28 Videos
- NUCLEI BOOK - NARAYNACHAPTER - NUCLEI EXERCISE - ASSERTION & REASON
5 Videos
- SEMI CONDUCTOR DEVICESBOOK - NARAYNACHAPTER - SEMI CONDUCTOR DEVICESEXERCISE - Level-II (H.W)
36 Videos
Similar Questions
A ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View SolutionA ray of light falls on a transparent sphere with centre at C as shown in figure. The ray emerges from the sphere parallel to line AB. The refractive index of the sphere is

View Solution
Knowledge Check
A parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
A32B53C2D52A parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
A32B53C2D52A ray of light incident on a transparent sphere at an angle π/4 and refracted at an angle r, emerges from the sphere after suffering one internal reflection. The total angle of deviation of the ray is
A3π2−4rBπ2−4rCπ4−rD5π2−4r
A parallel beam of light emerges from the opposite surface of the sphere when a point source of light lies at the surface of the sphere. The refractive index of the sphere is
View SolutionA point source of light is kept on the surface of a sphere and it is found that parallel light rays emerge from the other side of the sphere. What is refractive index of material of the sphere ?
View SolutionParallel rays are incident on a transparent sphere along its one diameter. After refraction, these rays converge at the other end of this diameter. The refractive index for the material of sphere is
View SolutionA poing source of light at the surface of a sphere causes a paralel beam of light to emerge from the opposite surface of the sphere. The refractive index of the material of the sphere is
View SolutionA ray of light passes through four transpar ent media with refractive indicesμ1,μ2,μ3 and μ4 as shown in figure. The surfaces of all media are parallel. If the emergent ray is parallel to the incident ray, we must hav
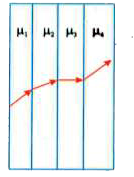
View Solution
