Gravitational field intensity at the centre of the semi circle formed by a thin wire AB of mass m and length L is

Gm2L2(ˆi)
Gm2πL2(ˆj)
2πGmL2(ˆi)
2πGmL2(ˆj)
The correct Answer is:D
dE=GdmR2=GλdθR
E=∫+π/2−π/wdEcosθ=2GλR
Topper's Solved these Questions
Similar Questions
Calculate the gravitational field intensity at the centre of the base of a hollow hemisphere of mass M and radius R. (Assume the base of hemisphere to be open)

View SolutionCalculate the gravitational field intensity at the centre of the base of a hollow hemisphere of mass M and radius R. (Assume the base of hemisphere to be open)

View Solution
Knowledge Check
If gravitational field Intensity is E at distance R/2 outside from then surface of a thin shell of radius R , the gravitational field intensity at distance R/2 from its centre is
AZeroB2EC2E3D3E2
Calculate the gravitational field intensity and potential at the centre of the base of a solid hemisphere of mass m, radius R
View SolutionCalculate the gravitational field intensity and potential at the centre of the base of a solid hemisphere of mass m, radius R
View SolutionCalculate gravitational field intensity at a distance x on the axis from centre of a uniform disc of mass M and radius R .
View SolutionIf gravitational field Intensity is E at distance R/2 outside from then surface of a thin shell of radius R , the gravitational field intensity at distance R/2 from its centre is
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionFind the intensity of gravitational field at a point lying at a distance x from the centre on the axis of a ring of radius a and mass M.
View SolutionFind the gravitational potential energy of a system consisting of a uniform rod AB of mass M, length l and a point mass m as shown in figure.
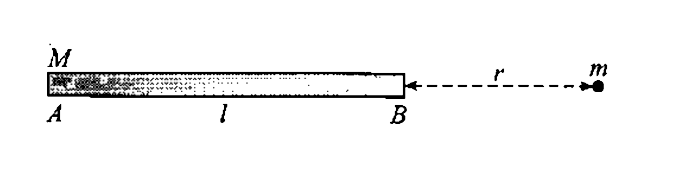
View Solution
