A particle suspended from a vetical spring oscillastes 10 times per sencon. At the highest point of oscillation the spring becomes unstretched. A. Find the maximum speed of the block. B. Find the speed when the spring is stretche by 0.20 cm. Take g=π2ms−2
a. The mea position of the particle durig vertical oscillsations is mgk distance away from its position when the sprig is unstretched. At the highest point i.e. at an extreme positon, the spring is unstretched.
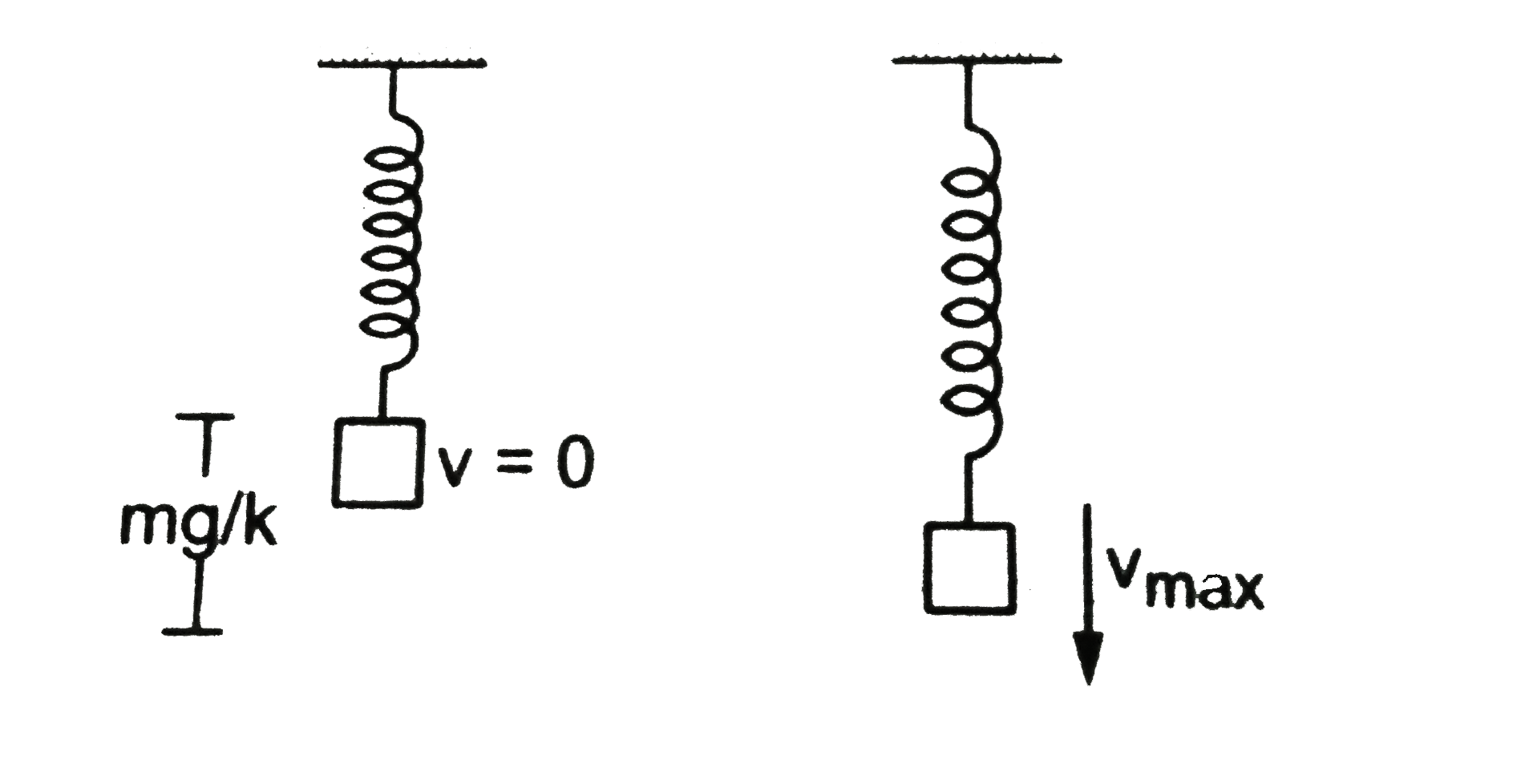
hence the amplitude is
A=mgk..............i
The angular frequency is
ω=√km=2πv=(20π)s−1........ii
or mk=140π2s2
Putting in i the amplitude is
A=(1400π2s2)(π2ms2)
=1400m=0.25cm
The maximum speed =Aω
k =(0.25cm)(20πs−1)=5πcms−1
b. When the spring is stretched by 0.20 cm the block is 0.25 cm-0.20 cm=0.05 cm above the meann position. The speed at this positioin will be
v=ω√A2−x2
=(20πs−1)(√(0.25cm)2−(0.05cm)2
=15.4cms−1
Topper's Solved these Questions
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Short Answer
13 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Objective 1
21 Videos
- SIMPLE HARMONIC MOTIONBOOK - HC VERMACHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Exercises
58 Videos
- ROTATIONAL MECHANICSBOOK - HC VERMACHAPTER - ROTATIONAL MECHANICSEXERCISE - Exercises
86 Videos
- SOME MECHANICAL PROPERTIES OF MATTERBOOK - HC VERMACHAPTER - SOME MECHANICAL PROPERTIES OF MATTEREXERCISE - Exercises
32 Videos
Similar Questions
A particle suspended from a vertical spring oscillates 10 times per second. At the highest point of oscillation , the spring becomes upstretched . Find the speed when the spring is stretched by 0.20 cm . (Take , g=π2m/s2)
View SolutionFrequency of a particle executing SHM is 10Hz. The particle is suspended form a vertical spring. At the highest point of its oscillation the spring is unstretched. Find the maximum speed of the particle: (g=10m/s2)
View Solution
Knowledge Check
A particle suspended from a vertical spring oscillates 8 times per second. At the highest point of oscillation the spring becomes unstretched. The maximum speed of the block will be
A10 cm/sB20 cm/sC30 cm/sD40 cm/sFrequency of a particle executing SHM is 10 Hz. The particle is suspended from a vertical spring. At the highest point of its oscillation the spring is unstretched. Maximum speed of the particle is (g=10m/s2
A2πm/sBπm/sC1πm/sD12πm/sFrequency of a particle executing SHM is 10 Hz. The particle is suspended from a vertical spring. At the highest point of its oscillation the spring is unstretched. Maximum speed of the particle is (g=10ms)
A2πmsBπmsC1πmsD12π/ms
The block shown in figure is released from rest. Find out the speed of the block when the spring is compressed by 1 m
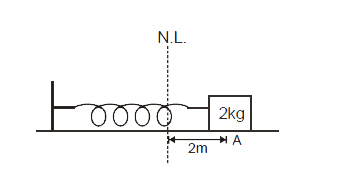
View SolutionIn the given arrangement the block is released from the position where the spring is unstretched. The speed of the block when it has descended through 2cm is x10. Find the value of x.
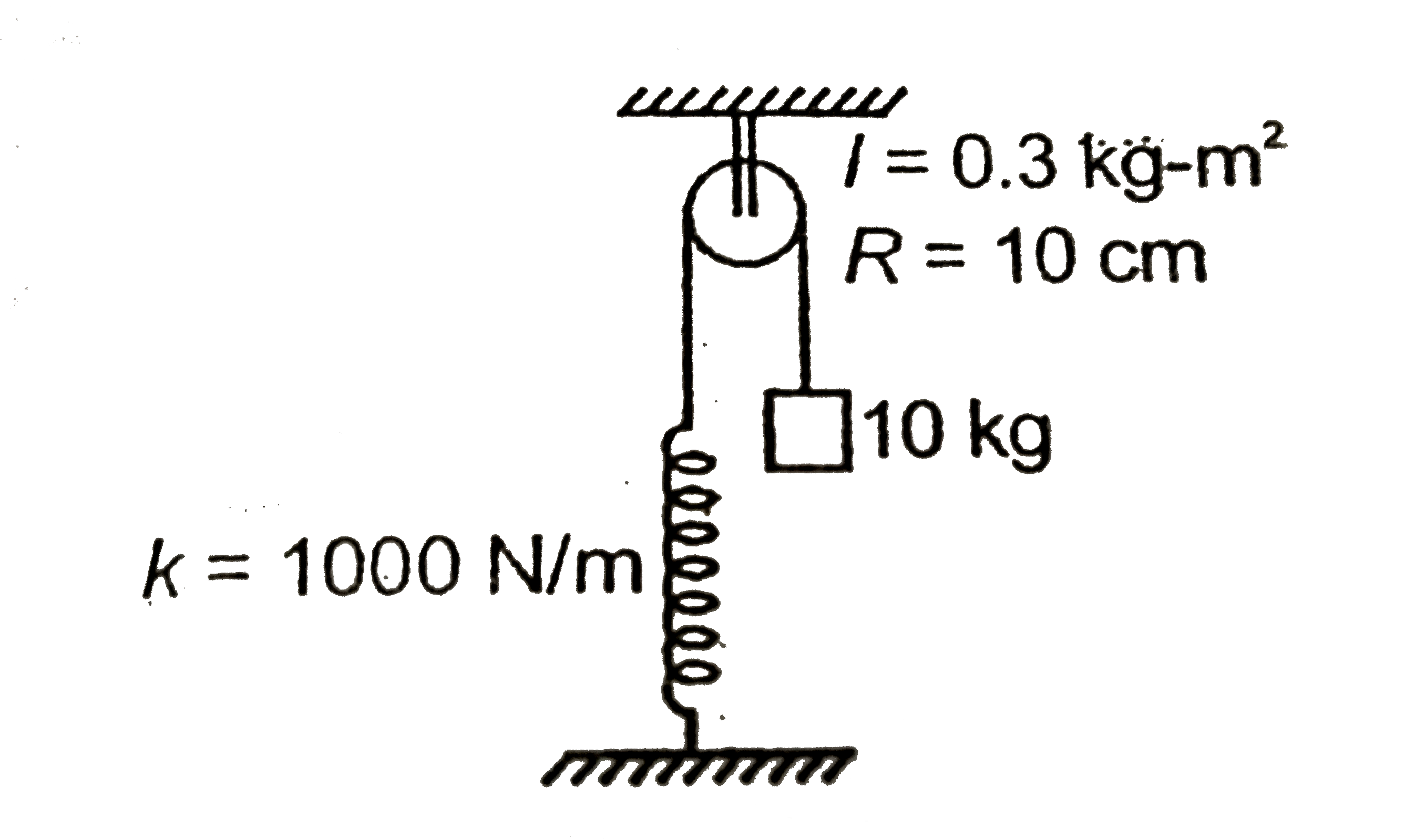
View SolutionA mass m suspended from a vertical spring oscillates with a period of 4 s. The mass is then kept at rest. Through what dis"tan"ce the spring will be stretched ? [Take pi^(2)=10]
View SolutionA mass is suspended from a vertica spring which is executing SHM of frequency 5 Hz.
The spring is unstretched at the highest point of oscillation. Maximum speed of the mass is (take, acceleration due to gravity, g=10m/s2 )
View SolutionA ball of mass 2kg hanging from a spring oscillates with a time period 2π seconds. Ball is removed when it is in equilibrium position, then spring shortens by
View Solution
