Three identical charges are placed on three vertices of a square. If the force acting between q1andq2 is F12 and between q1andq3 is F13 then F13F12= ________.
12
2
1√2
√2
The correct Answer is:A
To solve the problem, we need to find the ratio of the forces F13 (the force between charges q1 and q3) and F12 (the force between charges q1 and q2) when the charges are placed at the vertices of a square.
1. Identify the Charges and Distances:
- Let the charges at the vertices of the square be q1, q2, and q3.
- The distance between q1 and q2 (which are adjacent vertices) is A (the side length of the square).
- The distance between q1 and q3 (which are opposite vertices) is A√2 (the diagonal of the square).
2. Apply Coulomb's Law:
- According to Coulomb's law, the force between two point charges is given by:
F=kq1q2r2
- For F12 (force between q1 and q2):
F12=kq2A2
- For F13 (force between q1 and q3):
F13=kq2(A√2)2=kq22A2
3. Calculate the Ratio F13F12:
- Now, we can find the ratio of the two forces:
F13F12=kq22A2kq2A2=1/21=12
4. Final Answer:
- Therefore, the ratio F13F12 is:
F13F12=12
- Let the charges at the vertices of the square be q1, q2, and q3.
- The distance between q1 and q2 (which are adjacent vertices) is A (the side length of the square).
- The distance between q1 and q3 (which are opposite vertices) is A√2 (the diagonal of the square).
- According to Coulomb's law, the force between two point charges is given by:
F=kq1q2r2
- For F12 (force between q1 and q2):
F12=kq2A2
- For F13 (force between q1 and q3):
F13=kq2(A√2)2=kq22A2
- Now, we can find the ratio of the two forces:
F13F12=kq22A2kq2A2=1/21=12
- Therefore, the ratio F13F12 is:
F13F12=12
Topper's Solved these Questions
Similar Questions
Three charges q1=1μC,q2=2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. Find the net electric force acting on charge q1

View SolutionFive identical charges, q1 each, are placed at the vertices of a regular pentagon having side length l1. The net electrostatic force on any of the charges due to other four is F1. Find the electrostatic force F2 on any one of the five identical charges, q2 each, placed at the vertices of a regular pentagon having side length l2.
View Solution
Knowledge Check
Three equal charges are placed on the three corners of a square. If the force between q1 and q2 is F12 and that between q1 and q3 is F13, then the ratio of magnitudes (F12/F13) is
A1/2B2C1/√2D√2Three charges +q, +q and -2q are placed at the vertices of an equilareral triagle. What is the dipole moment of the system?
A√3qaB√3qa2C√2qaDqa2Three point charges each of value +q are placed on three vertices of a square of side a metre. What is the magnitude of the force on a point charge of value −q coulomb placed at the centre of the square?
A(14πε0)(qa)2B(12πε0)(2qa)2C(12πε0)(qa)2D(14πε0)(2qa)2
Three charges q1=1μC,q2=−2μC and q3=3μC are placed on the vertices of an equilateral triangle of side 1.0 m. find the net electric force acting on charge q1.
How to proceed Charge q2 will attract charge q1 (along the line joining them) and charge q3 will repel charge q1. Therefore, two forces will act on q1, one due to q2 and another due to q3. Since , the force is a vector quantity both of these force (say F1 and F2) will be added by vector method. Following are two methods of their addition

View SolutionThree point charges +q, +2q and Q are placed at the three vertices of an equilateral triangle. Find the value of charge Q (in terms of q), so that electric potential energy of the system is zero.
View SolutionThree charges −q1, +q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
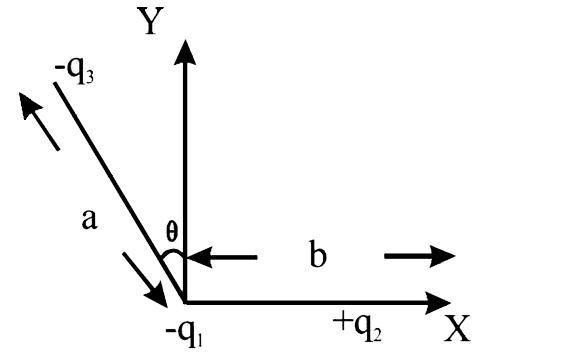
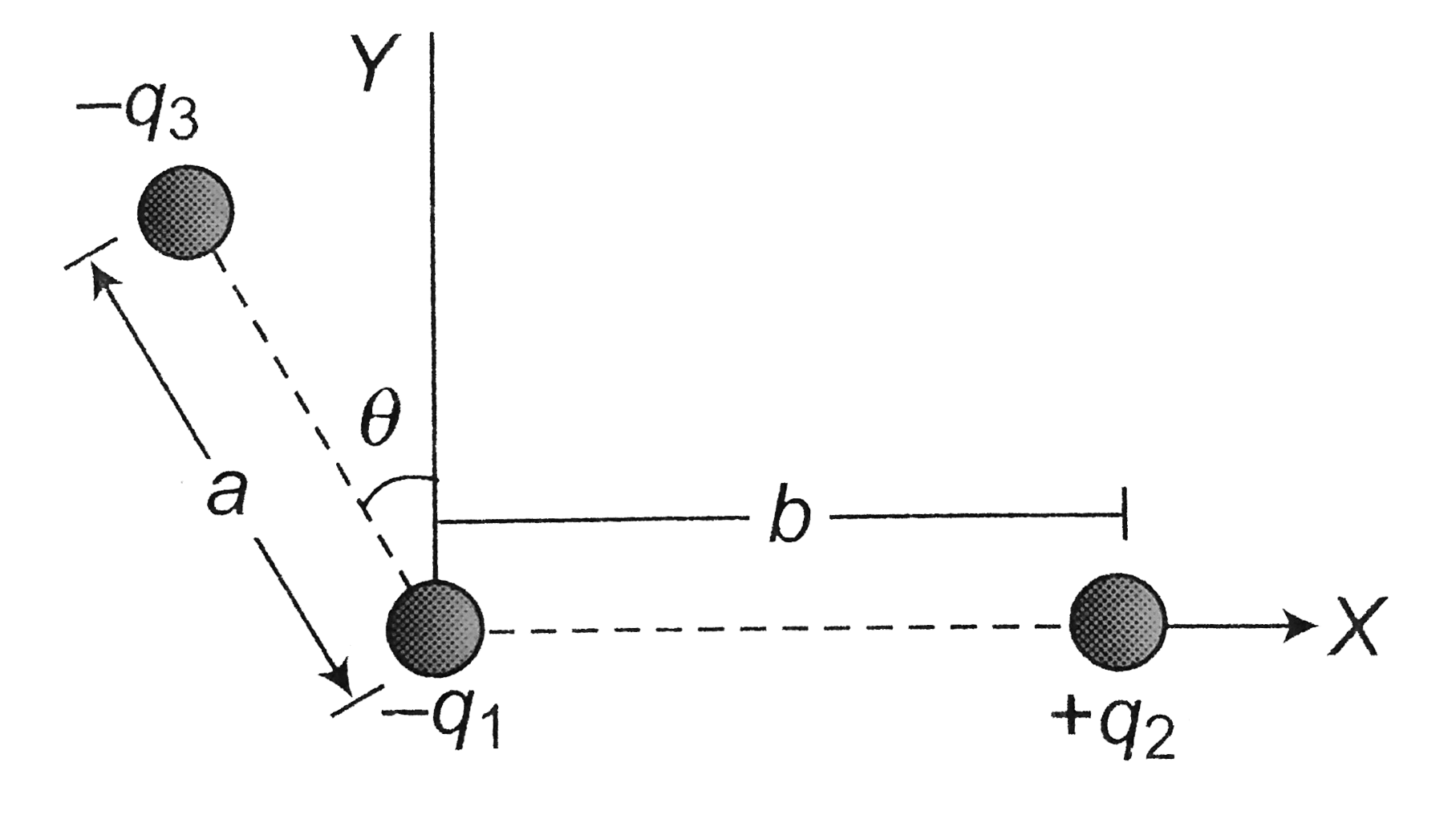
View SolutionThree charges −q1,+q2 and −q3 are placed as shown in the figure. The x-component of the force on −q1 is proportional to
View SolutionThree charges are placed at the vertices of an equilateral triangle of side 10 cm. Assume q1=1μC,q2=−2μCandq3=4μC. Work done in separating the charges to infinity is
View Solution
