If A=[ab0a] is nth root of I2, then choose the correct statements: If n is odd, a=1,b=0 If n is odd, a=−1,b=0 If n is even, a=1,b=0 If n is even, a=−1,b=0 a. i, ii, iii, iv b. ii, iii, iv c. i, ii, iii, iv d. i, iii, iv
To solve the problem, we need to determine the conditions on the elements a and b of the matrix A=(ab0a) such that An=I2, where I2 is the identity matrix of order 2.
1. Understanding the Matrix:
The matrix A is given as:
A=(ab0a)
We need to find An.
2. Calculating A2:
To find An, we first calculate A2:
A2=A⋅A=(ab0a)(ab0a)=(a2ab+ba0a2)=(a2ab0a2)
3. Calculating A3:
Next, we calculate A3:
A3=A2⋅A=(a2ab0a2)(ab0a)=(a3a2b+aba0a3)=(a32a2b0a3)
4. General Form of An:
Continuing this pattern, we can deduce that:
An=(annan−1b0an)
5. Setting An=I2:
For An to equal the identity matrix I2:
An=(1001)
This gives us two conditions:
- an=1
- nan−1b=0
6. Analyzing the Conditions:
- From an=1:
- If n is odd, a can be either 1 or −1.
- If n is even, a must be 1 (since −1 raised to an even power is 1).
- From nan−1b=0:
- If a≠0, then b must be 0.
7. Conclusion:
- If n is odd, a can be 1 or −1 and b=0.
- If n is even, a must be 1 and b=0.
Summary of Statements:
- If n is odd, a=1,b=0 (True)
- If n is odd, a=−1,b=0 (True)
- If n is even, a=1,b=0 (True)
- If n is even, a=−1,b=0 (False)
Final Answer:
The correct statements are:
- i, ii, iii (d)
The matrix A is given as:
A=(ab0a)
We need to find An.
To find An, we first calculate A2:
A2=A⋅A=(ab0a)(ab0a)=(a2ab+ba0a2)=(a2ab0a2)
Next, we calculate A3:
A3=A2⋅A=(a2ab0a2)(ab0a)=(a3a2b+aba0a3)=(a32a2b0a3)
Continuing this pattern, we can deduce that:
An=(annan−1b0an)
For An to equal the identity matrix I2:
An=(1001)
This gives us two conditions:
- an=1
- nan−1b=0
- From an=1:
- If n is odd, a can be either 1 or −1.
- If n is even, a must be 1 (since −1 raised to an even power is 1).
- From nan−1b=0:
- If a≠0, then b must be 0.
- If n is odd, a can be 1 or −1 and b=0.
- If n is even, a must be 1 and b=0.
- If n is odd, a=1,b=0 (True)
- If n is odd, a=−1,b=0 (True)
- If n is even, a=1,b=0 (True)
- If n is even, a=−1,b=0 (False)
The correct statements are:
- i, ii, iii (d)
Similar Questions
Knowledge Check
Find the odd one out.
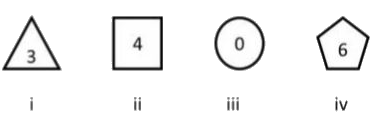
A. iii
B. ii
C. i
D. ivAABBCDDC
If p+iq=0 then p+q is (i) 1 (ii)−1 (iii)−2 (iv)0
View SolutionThe Additive inverse of 1/2 is
i. -2
ii. -1/2
iii. 1/2
iv. 0
View SolutionMatch the statements (a, b, c, d) in column I with the statements (I, ii, iii, iv) in column II.

View SolutionMatch the statements (a, b, c, d) in column I with the statements (I, ii, iii, iv) in column II.
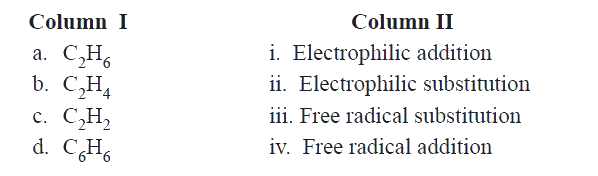
View SolutionFor the integer n , if n3 is odd, then which of the following statements are true? n is odd. II. n2 is odd. III. n2 is even (a) I only (b) II only (c) I and II only (d) I and III only
View Solutionmatch the staements (a,b,c,d) in column I with the statements(I,ii,iii,iv) in column II

View Solutionmatch the staements (a,b,c,d) in column I with the statements(I,ii,iii,iv) in column II
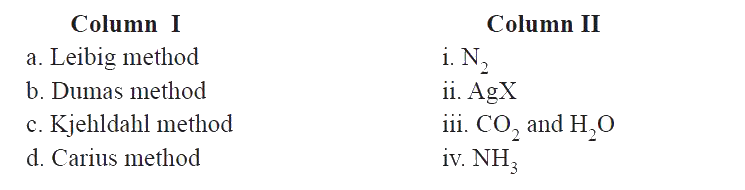
View Solution

