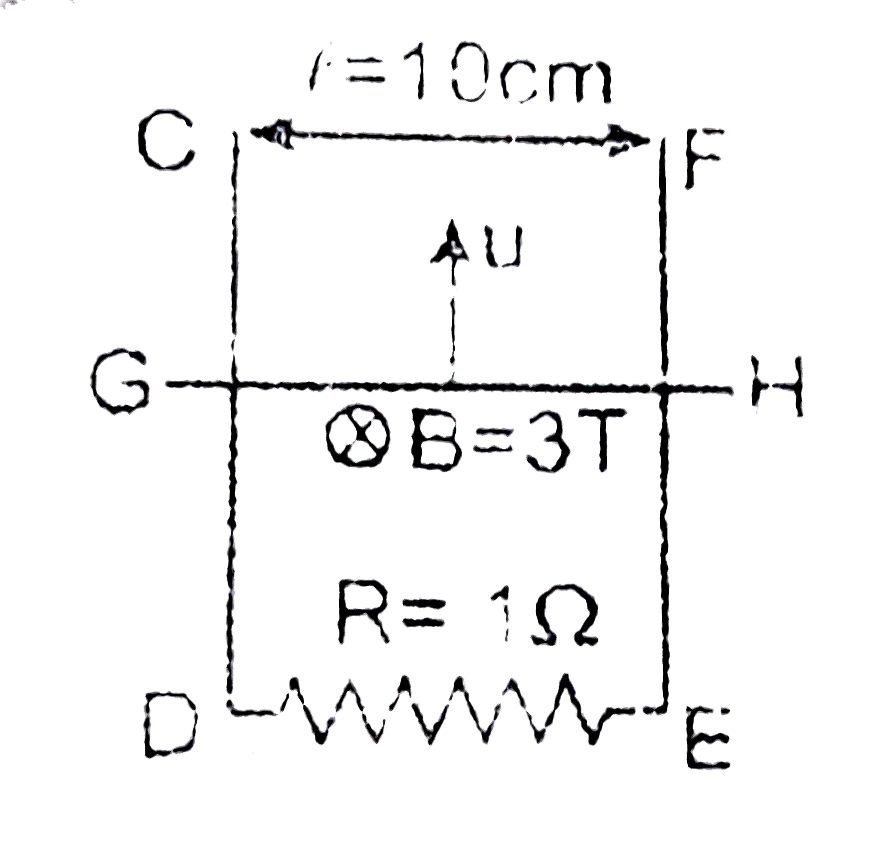
In the figure, CDEF is a fixed conducting smooth frame in vertical plane.A conducting uniform rod GH of mass m=1g can move vertically and smoothly without losing contact with the frame.GH always remains horizontal.It is given velocity u=1m/s upwards and released.Taking the acceleration due to gravity as g and assuming that no resistance is present other than R.Time taken by rod to reach the highest point is equal to ln10x second.Find out value of x.
The correct Answer is:90
Step by step video, text & image solution for In the figure, CDEF is a fixed conducting smooth frame in vertical plane.A conducting uniform rod GH of mass m=1 g can move vertically and smoothly without losing contact with the frame.GH always remains horizontal.It is given velocity u=1m//s upwards and released.Taking the acceleration due to gravity as g and assuming that no resistance is present other than R.Time taken by rod to reach the highest point is equal to (ln10)/x second.Find out value of x. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 3
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 4
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
15 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - HLP
39 Videos
Similar Questions
CDEF is a fixed conducting smooth frame in vertical plane. A conducting uniform rod GH of mass m can move vertically and smoothly without losing contact with the frame. Gh always remains horizontal and is given velocity u upward and released. Taking the acceleration due to gravity as g and present other than R. Find out the time tasken by the rod to reach the highest point.

View SolutionA particle is projected vertically upwards from ground with velocity 10 m/s. Find the time taken by it to reach at the highest point ?
View Solution
Knowledge Check
A rocket is fired vertically upwards and moves with net acceleration of 10m/s2. After 1 min the fuel is exhausted. The time taken by it to reach the highest point after the fuel is exhausted will be:
A10 secB20 secC30 secD60 secThe maximum height reached by projectile is 4m. The horizontal range is 12m. The velocity of projection in ms−1 is (g is acceleration due to gravity)
A5√g/2B3√g/2C13√g/2D15√g/2The ratio ggh, where g and gh are the acceleration due to gravity at the surface of the earth and at a height h above the earth's surface respectively, is :
A(1+hR)2B(1+Rh)2C(Rh)2D(hR)2
An object is thrown vertically upwards and rises to a height of 10 m. Calculate
(i) the velocity with which the object was thrown upwards and (ii) the time taken by the object to reach the highest point.
View SolutionIn the figure shown PQRS is a fixed resistanceless conducting frame in a uniform and constant magnetic field of strength B. A rod EF of mass m length l and resistance R can smoothly move on this frame.A capacitor charged to a potential difference V0 initially is connected as shown in the figure.Find the velocity of the rod as function of time t if it is released at t=0 from rest.
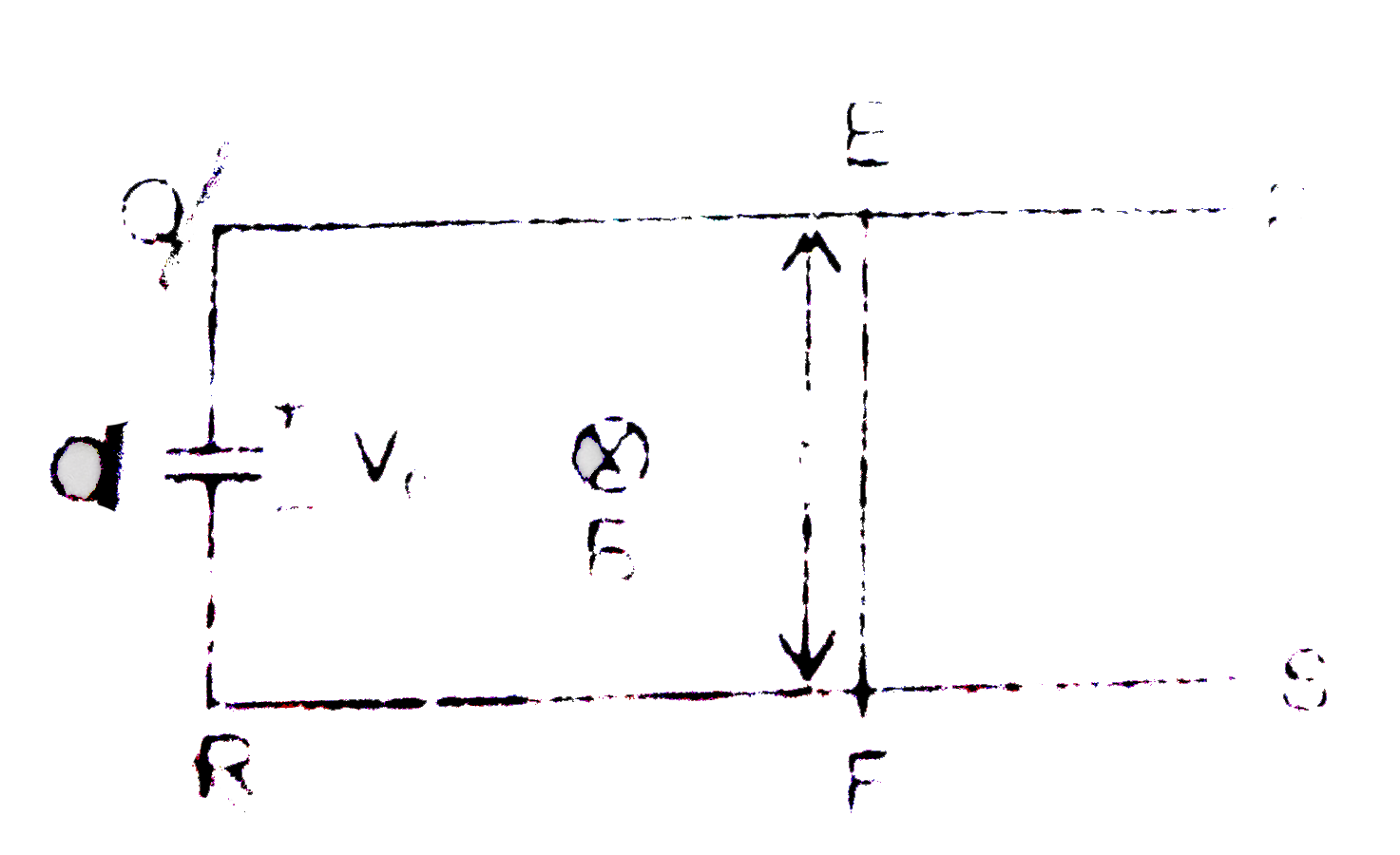
View SolutionA uniform rod of mass m and length l can rotate in a vertical plane about a smooth horizontal axis point H. a. Find angular acceleration α of the rod. just after it is released from initial horizontal position from rest'? b. Calculate the acceleration (tangential and radial) , point A at this moment.
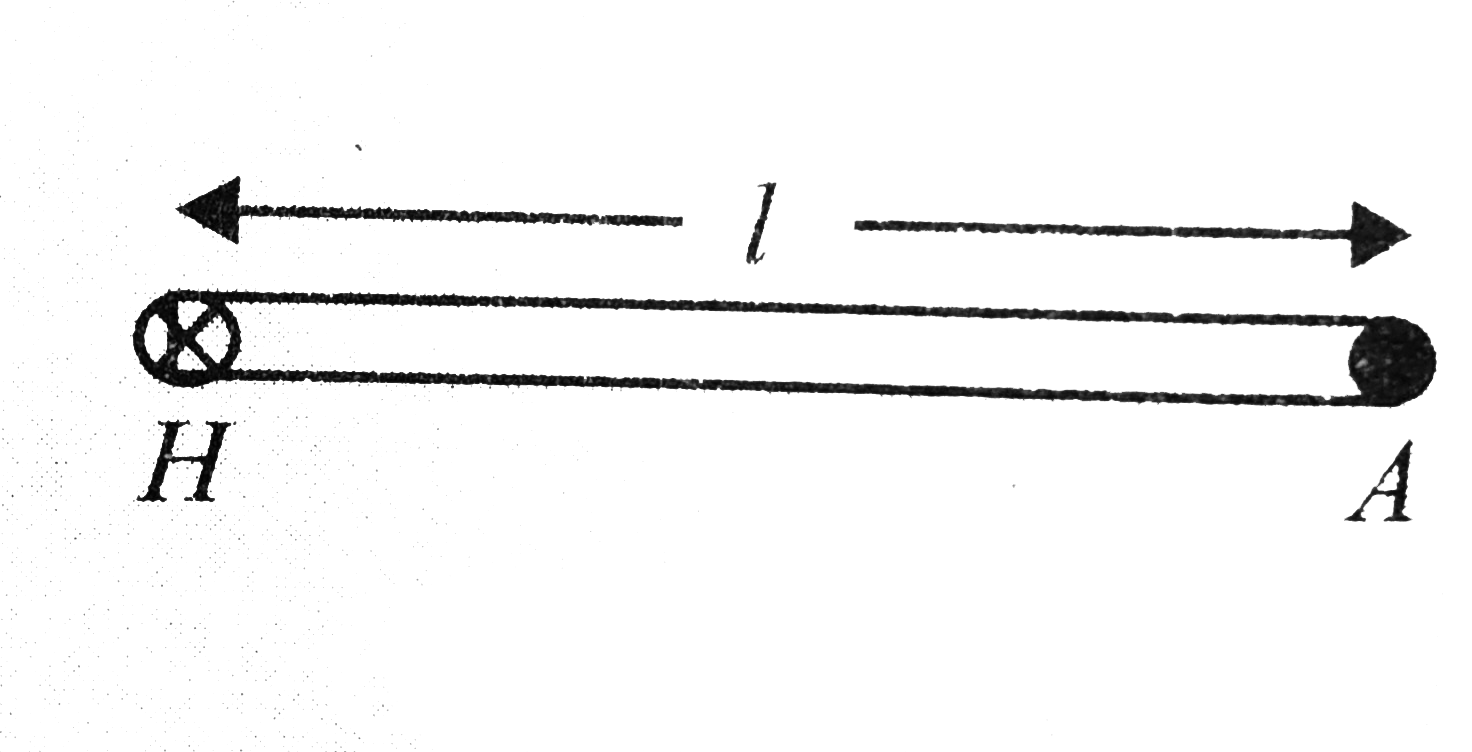
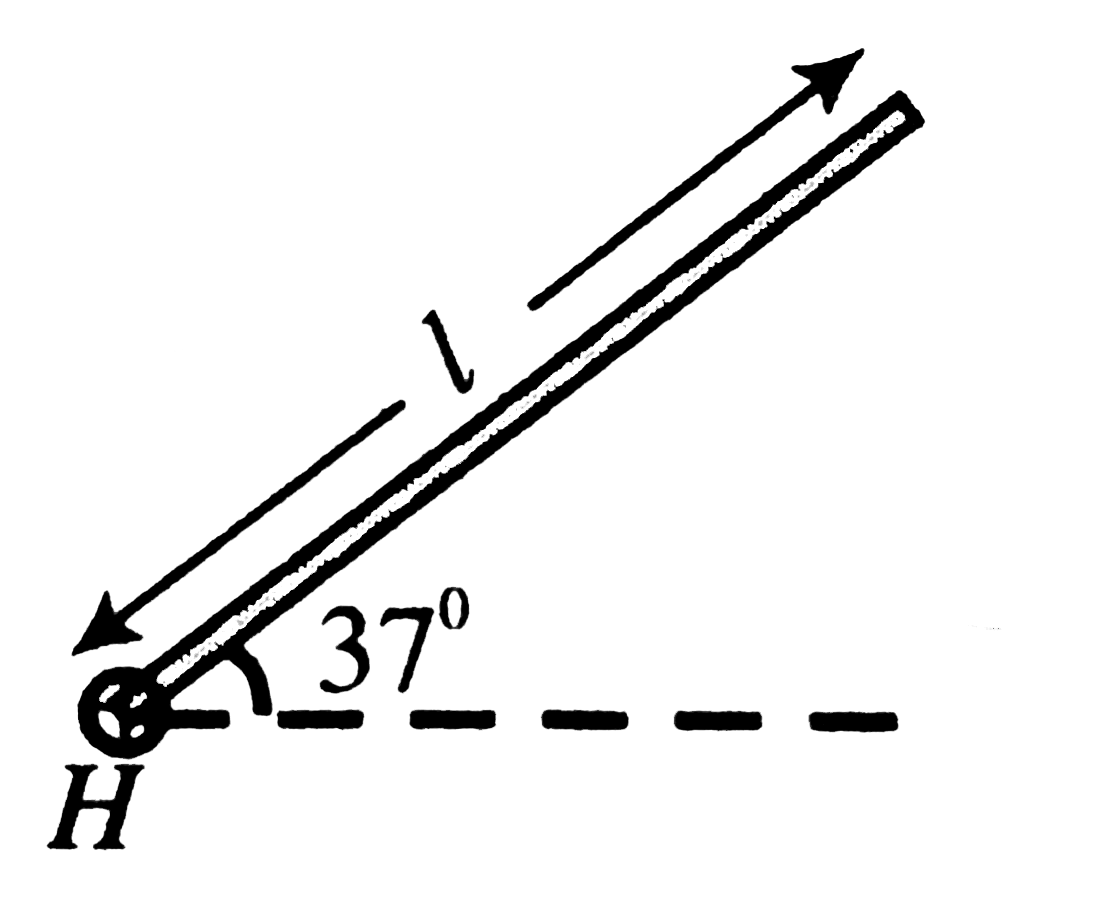
View SolutionA uniform rod of mass m and length l can rotate in vertical plane about a smooth horizontal axis hinged at point H. Find angular acceleration α of the rod just after it is released from initial position making an angle of 37∘ with horizontal from rest?
View SolutionThe ratio ggh, where g and gh are the acceleration due to gravity at the surface of the earth and at a height h above the earth's surface respectively, is :
View Solution