A long straight wire carries a current I0, at distance a and b=3a from it there are two other wires, parallel to the former one, which are interconnected by a resistance R(figure).A connector slides without friction along the wires with a constant velocity v.Assuming the resistance of the wires,the connector, the sliding contacts and the self-inductance of the frame to be negligible. The point of application (distance from the long wire) of magnetic force on sliding wire due to the long wire is 2alnx from long wire.Then find out value of x.
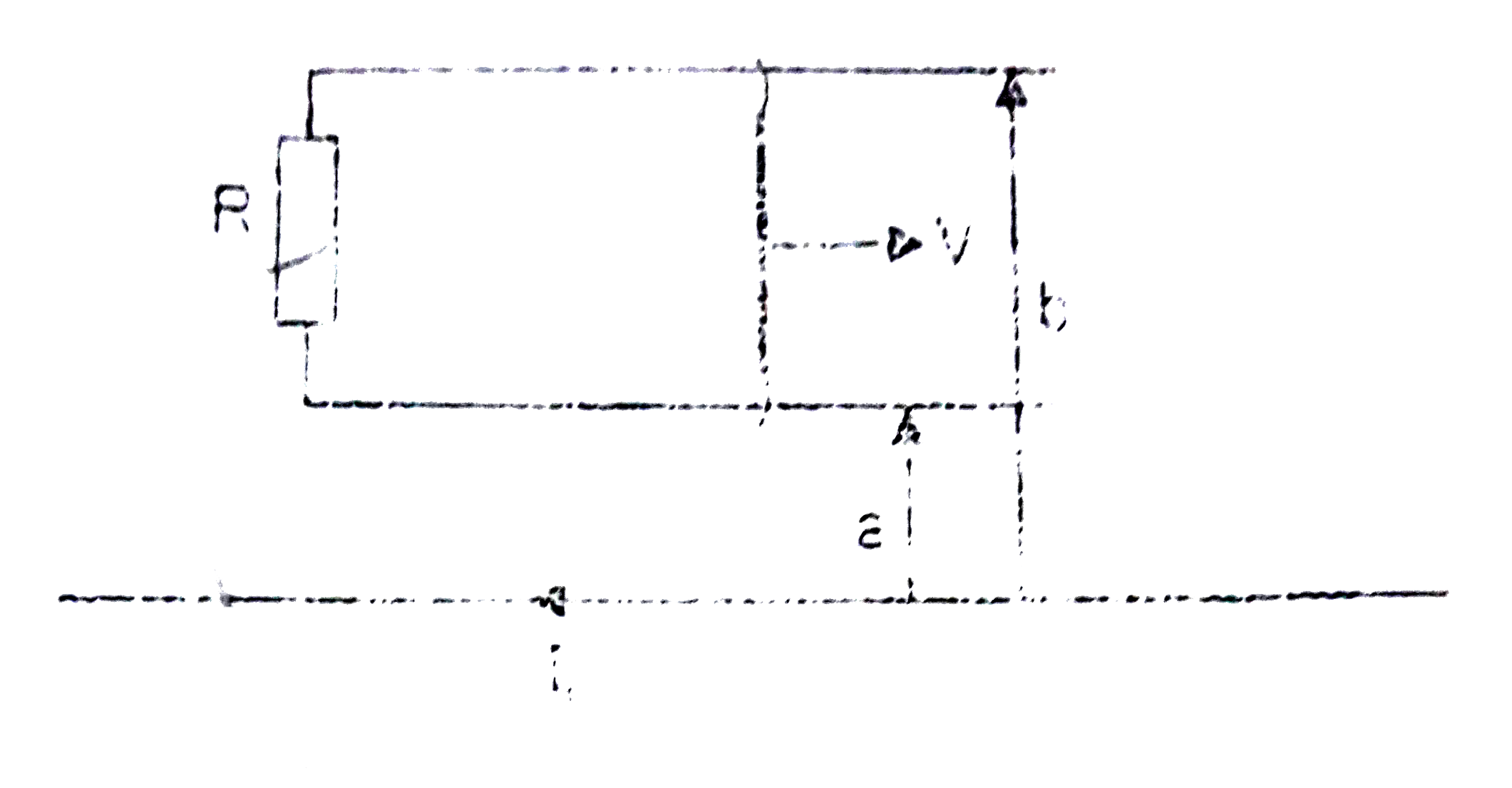
The correct Answer is:C
∫(Torque of elecentary force)=Torque of net force.
μ0I02πI∫xdxx=F0¯x=μ0I02πIln(ba)¯x⇒¯x=b−aln(b/a)⇒¯x=2aln3⇒x=3
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 3
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 4
6 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
15 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - HLP
39 Videos
Similar Questions
A long straight wire carries a current I0. At distance a and b =3a from it there are two other wires, parallel to the former one, which are interconnected by a resistance R ( figure ). A connector slides without friction along the wire with a constant velocity v. Assuming the resistance of the wire, the connector, the sliding contact, and the self-inductance of the frame to be negligible ,
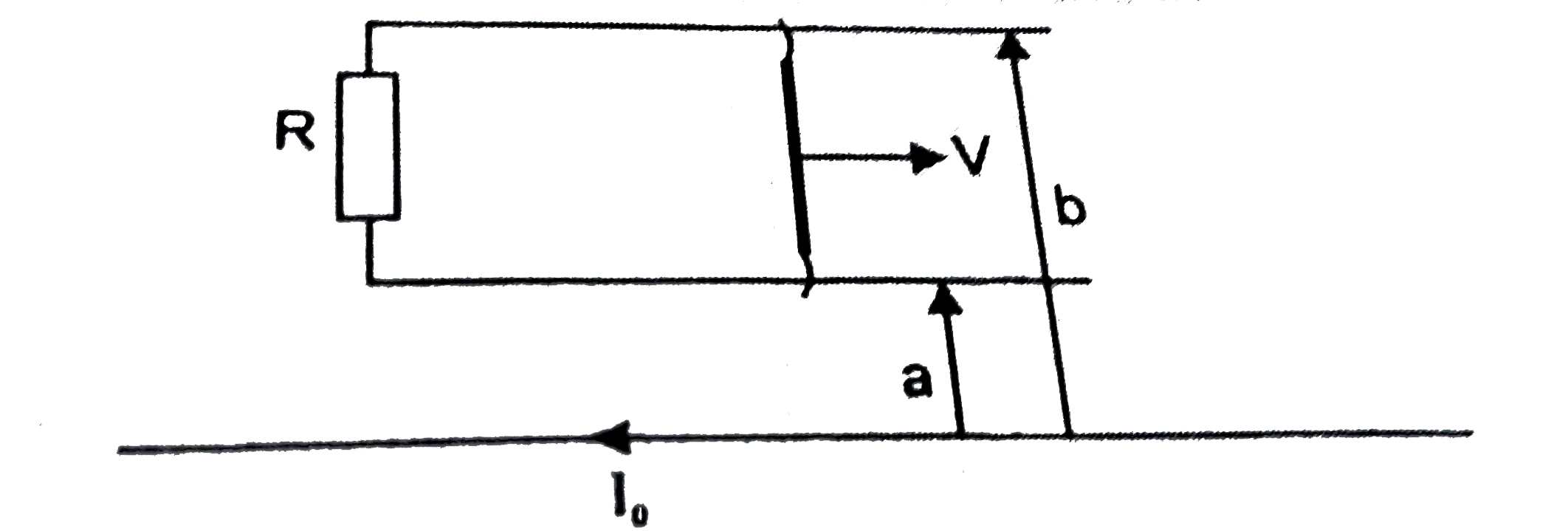
The point of application (distance from the long wire ) of magnetic force on sliding wire due to the long wire is 2alnx from long wire. Then findout value of x.
View SolutionA long straight wire carries a current I0. At distances a and b from it there are two other wires, parallel to the former one, which are interconnected by a resistance R (Fig). A connector slides without friction along the wires with a constant velocity v. Assuming the resistances of the wires, the conductor, the sliding contacts, and the self-inductance of the frame to be negligable, find:
(a) the magnitude and the direction of the current induced in the connector,
(b) the force required to maintain the connector's velocity constant.

View Solution
Knowledge Check
If a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5TIf a long straight wire carries a current of 40 A, then the magnitude of the field B at a point 15 cm away from the wire is
A5.34×10−5TB8.34×10−5TC9.6×10−5TD10.2×10−5T
An infinitely long straight wire carrying current I , one side opened rectangular loop and a conductor C with a sliding connector are located in the same plane , as shown in the figure. The connector has length l and resistance R . It slides of the right with a velocity v. The resistance of the conductor and the self inductance of the loop are negligible . The induced current in the loop , as function of separation r between the conductor and the straight wire is :
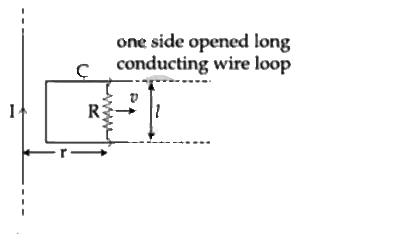
View SolutionAn infinitely long straight wire carrying current I , one side opened rectangular loop and a conductor C with a sliding connector are located in the same plane , as shown in the figure. The connector has length l and resistance R . It slides of the right with a velocity v. The resistance of the conductor and the self inductance of the loop are negligible . The induced current in the loop , as function of separation r between the conductor and the straight wire is :

View SolutionA long straight wire carrying a current I and a II- shaped conductor with siding connector are located in the same plane as shown in Fig. The connector of length l and resistance R sides to the right with a current induced in the loop as a function of separation r between the connector and the stragiht wire. The resistance of the II-shaped conductor and the self-induced of the loop are assumed to be negligible.

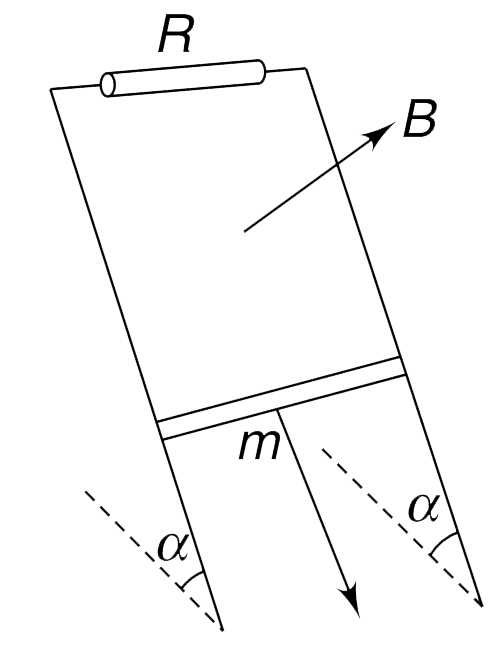
View SolutionA copper connector of massm, starting from rest, slides down two conducting bars set at angle α to the horizontal, due to gravity (see figure). At the top the bars are interconnected trhough a resistance R. The separation between the bars is equal to l. The system is located in uniform magnetic field of induction B, perpendicular to the plane in which the connectr slides. The resistance of the bars the connector and the sliding contacts, as well as the self inductance of the loop, are assumed to be negligible. The coefficient of friction between the connector and the bars is equal to 12 and α
(a) Find the steady-state velocity of the connector.
(b) How will your answer differ if the magnetic field was in opposite direction.
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v. Find the emf induced in the wire when its distance in the wire when its distance from the long wire is x.
View SolutionA rod of length l is kept parallel to a long wire carrying constant current i . It is moving away from the wire with a velocity v.F∈dtheemf∈duced∈thewirewhenitsdistance∈thewirewhenitsdistanceomthelongwireisx.
View Solution
