A mass of 1kg attached to the bottom of a spring has a certain frequency of vibration. The following mass has to be added to it in order to reduce the frequency by half :
1kg
2kg
3kg
4kg
The correct Answer is:C
To solve the problem of how much mass needs to be added to reduce the frequency of a mass-spring system by half, we can follow these steps:
Step 1: Understand the frequency formula
The frequency of a mass-spring system is given by the formula:
F=12π√km
where:
- F is the frequency,
- k is the spring constant,
- m is the mass attached to the spring.
Step 2: Define the initial conditions
Let:
- m1=1kg (the initial mass),
- F1 be the initial frequency.
Using the frequency formula, we can express F1 as:
F1=12π√km1=12π√k1=12π√k
Step 3: Define the new conditions
Let m2 be the new mass after adding an additional mass m:
m2=m1+m
We want to reduce the frequency to half, so:
F2=F12
Step 4: Write the equation for the new frequency
Using the frequency formula for the new mass:
F2=12π√km2=12π√km1+m
Setting F2=F12:
12π√km1+m=12(12π√k)
Step 5: Simplify the equation
Cancel 12π from both sides:
√km1+m=12√k
Squaring both sides gives:
km1+m=14k
Now, we can cancel k (assuming k≠0):
1m1+m=14
Step 6: Solve for m1+m
Cross-multiplying gives:
1=14(m1+m)
Thus:
m1+m=4
Step 7: Solve for the additional mass m
Substituting m1=1kg:
1+m=4
So:
m=4−1=3kg
Final Answer
The mass that needs to be added is:
3kg
The frequency of a mass-spring system is given by the formula:
F=12π√km
where:
- F is the frequency,
- k is the spring constant,
- m is the mass attached to the spring.
Let:
- m1=1kg (the initial mass),
- F1 be the initial frequency.
F1=12π√km1=12π√k1=12π√k
Let m2 be the new mass after adding an additional mass m:
m2=m1+m
We want to reduce the frequency to half, so:
F2=F12
Using the frequency formula for the new mass:
F2=12π√km2=12π√km1+m
Setting F2=F12:
12π√km1+m=12(12π√k)
Cancel 12π from both sides:
√km1+m=12√k
Squaring both sides gives:
km1+m=14k
Now, we can cancel k (assuming k≠0):
1m1+m=14
Cross-multiplying gives:
1=14(m1+m)
Thus:
m1+m=4
Substituting m1=1kg:
1+m=4
So:
m=4−1=3kg
The mass that needs to be added is:
3kg
Topper's Solved these Questions
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - I26videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 2, PART - II1videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Exercise- 1, PART - I25videos
SIMPLE HARMONIC MOTION
- BOOK - RESONANCECHAPTER - SEMICONDUCTORSEXERCISE - Exercise 388videos
SEMICONDUCTORS
- BOOK - RESONANCECHAPTER - TEST PAPERSEXERCISE - FST-330videos
TEST PAPERS
Similar Questions
Knowledge Check
- Question 1 - Select One
Ultrasound has frequency of vibration
Abetween 20 and 20,000 HzBbelow 20 HzCabove 20,000 HzDbetween 500 and 10,000 Hz - Question 2 - Select One
Ultrasound has frequency of vibration
A20 HzBbetween 20 to 20,000 HzCabove 20,000 HzDless than 20 Hz - Question 3 - Select One
Which of the following tools has a spring attached to it?
AHacksawBViceCTin cutterDDrilin
A mass m attached to a spring A has a frequency of 3 Hz and a spring B has a frequency of 4 Hz.When both spring are connected as shown in the figure, Find the frequency (in Hz)of oscillation.
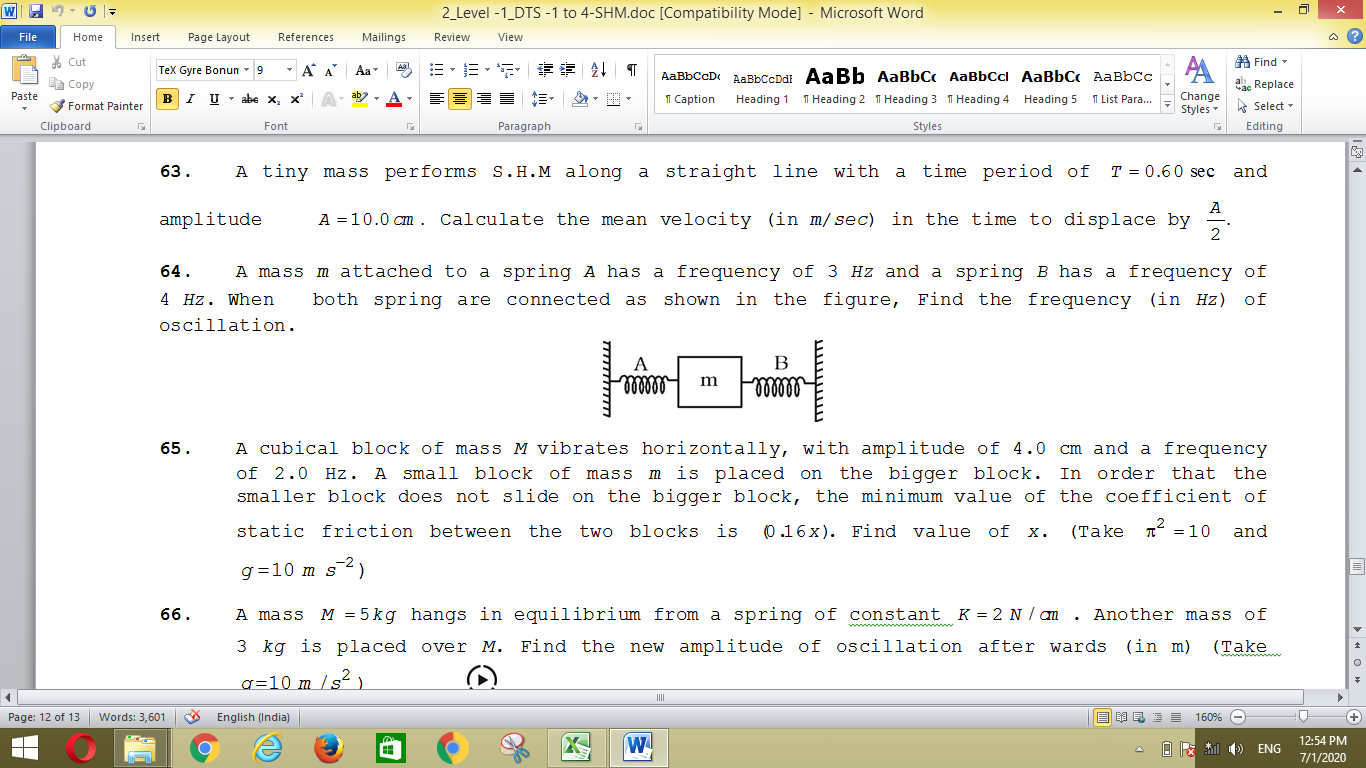 View Solution
View SolutionOn suspending a mass m from a spring of force constant k, frequency of vibration f is obtained. If a second spring as shown in the figure, is arranged then the frequency will be :
 View Solution
View SolutionWhich of the following tools has a spring attached to it?
View SolutionA mass m is suspended from a spring of length l and force constant K . The frequency of vibration of the mass is f1. The spring is cut into two equal parts and the same mass is suspended from one of the parts. The new frequency of vibration of mass is f2 . Which of the following relations between the frequencies is correct
View SolutionA spring mass system oscillates with a frequency n .If it is taken in an elavator slowly accelerating upward, the frequency will
View Solution

