A gaseous system changes from state A(P1,V1,T1) to B(P2,V2,T2) to C(P3,V3,T3) and finally from C to A. The whole process may be called :
Reversible process
Cyclic process
Isobaric process
Spontaneous process
The correct Answer is:B
Step by step video, text & image solution for A gaseous system changes from state A (P_(1), V_(1),T_(1)) to B (P_(2), V_(2),T_(2)) to C(P_(3), V_(3),T_(3)) and finally from C to A. The whole process may be called : by Chemistry experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- THERMODYNAMICSBOOK - RESONANCECHAPTER - THERMODYNAMICSEXERCISE - Exercise -2 Part-I: Only one option correct type
23 Videos
- THERMODYNAMICSBOOK - RESONANCECHAPTER - THERMODYNAMICSEXERCISE - Exercise-2 II: Single and double value integer type
16 Videos
- THERMODYNAMICSBOOK - RESONANCECHAPTER - THERMODYNAMICSEXERCISE - H-1
1 Videos
- TEST SERIESBOOK - RESONANCECHAPTER - TEST SERIESEXERCISE - CHEMISTRY
50 Videos
Similar Questions
Knowledge Check
A gaseous system changes from state A(P1,V1,T1) to B(P2,V2,T2), B to C (P3,V3T3) and finally from C to A. The whole process may be called
ACyclic processBReversible processCIsobaric processDSpontaneous processA gaseous system changes from state A(P1,V1,T1) to B(P2,V2,T2), B to C(P3,V3,T3) and finally from C to A. The whole process may be called
AReversible processBCyclic processCIsobaric processDSpontaneous process.P1V1T1=P2V2T2 is -
ABoyle's LawBCombined gas lawCCharles LawDNone of these
An ideal gas follows a process described by PV2=C from (P1,V1,T1) to (P2,V2,T2) (C is a constant). Then
View SolutionA system changes from the state (P1,V1) to (P2V2) as shwon in the diagram. The workdone by the system is
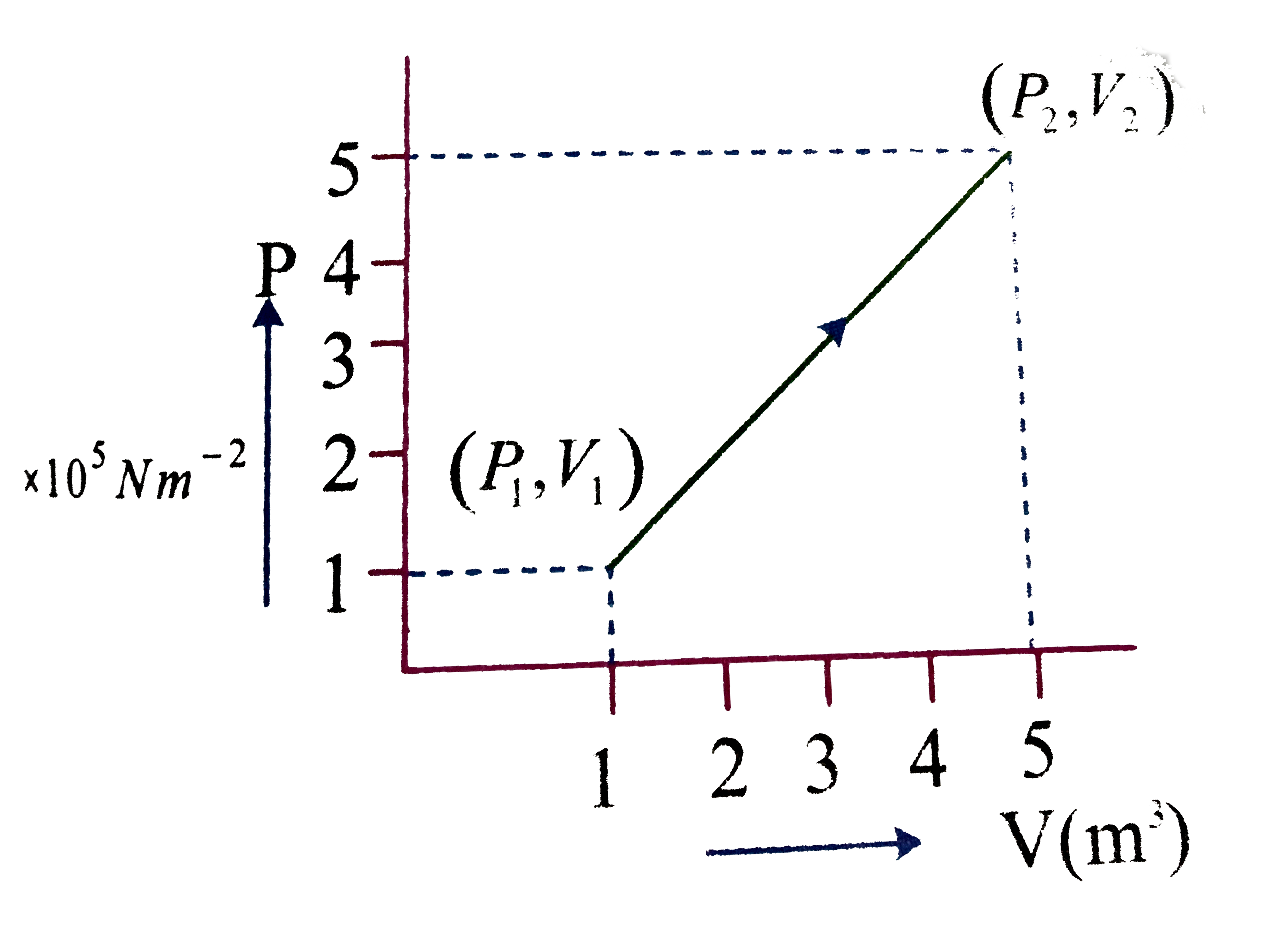
View SolutionA system changes from the state (P1,V1) to (P2,V2) as shown in the figure below. What is the work done by the system –
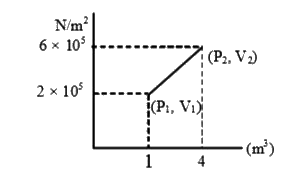
View SolutionAn ideal gas expands from state (P1,V1) to state (P2,V2), where P2=2P1 and V2=2V1. The path of the gas is expressed by the following relation,
P=P1[1+(V−V1V1)2]
View SolutionFor an ideal gas, an illustration of the different paths, A (B+C) and (D+E) from an intial state P1,V1,T1 to a final state P2,V2,T1 as shown in the given figure.

Path (A) represents a reversible isothernal expanison from P1V1 to P2V2. Path (B+C) represents a reversible adiabatic expansion (B) from P1,V1,T1 to P3,V2,T2 followed by reversible heating the gas at constant volume (C) from P3,V2,T2 to P2,V2T1 to P1,V2,T3 followed by reversible cooling at a constant volume V2 (E) from P1,V2,T3 to P2,V2,T1
What is ΔS for path (D+E) ?
View Solution
