A solid shere of radius R carries a charge Q distributed uniformly over its valume. A very small point like piece of it of mass m gets detached from the bottom of the sphere and falls down vertically under gravity. This piece carries charge q. If it acquires a speed v when it has fallen through a vertical height y (seefigure), then :(assume the remaining protion to be spherical).

v2=y[qQ4π∈0R2ym+g]
v2=y[qQ4π∈0R(R+y)m+g]
v2=2y[qQR4π∈0(R+y)3m+g]
v2=2y[qQ4π∈9R(R+y)m+g]
Step by step video & image solution for A solid shere of radius R carries a charge Q distributed uniformly over its valume. A very small point like piece of it of mass m gets detached from the bottom of the sphere and falls down vertically under gravity. This piece carries charge q. If it acquires a speed v when it has fallen through a vertical height y (seefigure), then :(assume the remaining protion to be spherical). by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
A hollow sphere of radius a carries a total charge Q distributed uniformly over its surface. A small area dA of the sphere is cut off. Find the electric field at the centre due to the remaining sphere.
View SolutionA circular wire loop of radius R carries a total charge q distributed uniformly over its length. A small length x(<<R) of the wire is cut off. Find the electric field at the centre due to the remaining wire.
View Solution
Knowledge Check
Consider a solid sphere of radius r and mass m which has a charge q distributed uniformly over its volume. The sphere is rotated about a diameter with an angular speed ω. The magnetic moment of the sphere is
A13qωr2B15qωr2C17qωr2D19qωr2A solid sphere of radius R has charge q uniformly distributed over its volume. The distance from it surfce at which the electrostatic potential is equal to half of the potential at the centre is
ARB2RCR3DR2A drop of water of mass m falls away from the bottom of charged conducting sphere of radius R, carrying with it a charge q1 and leaving the sphere a uniformly distributed charge q2. The kinetic energy of the drop after it has fallen height h is -
A14πξ0q1q2(hR(R+h))BmghC14πξ0q1q2(hR(R+h))+mghD14πξ0q1q2h+mgh
A spherical shell of radius r carries a uniformly distributed surface charge q on it. A hemispherical shell of radius R(gt r) is placed covering it with its centre coinciding with that of the sphere of radius r. The hemisphere has a uniform surface charge Q on it. The charge distribution on the sphere and the hemisphere is not affected due to each other. Calculate the force that the sphere will exert on the hemisphere.

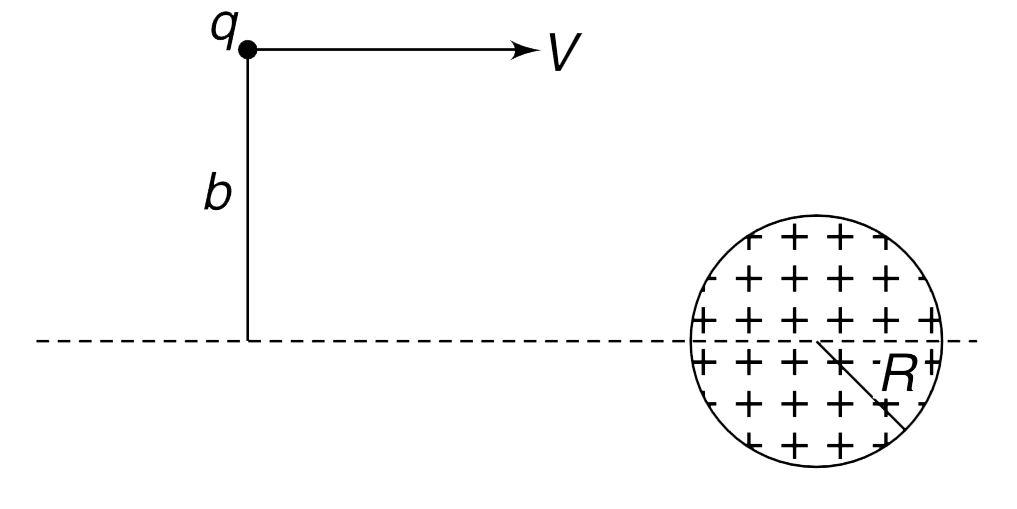
View SolutionThere is a fixed sphere of radius R having positive charge Q uniformly spread in its volume. A small particle having mass m and negative charge (–q) moves with speed V when it is far away from the sphere. The impact parameter (i.e., distance between the centre of the sphere and line of initial velocity of the particle) is b. As the particle passes by the sphere, its path gets deflected due to electrostatics interaction with the sphere.
(a) Assuming that the charge on the particle does not cause any effect on distribution of charge on the sphere, calculate the minimum impact parameter b0 that allows the particle to miss the sphere. Write the value of b0 in term of R for the case
12mV2=100.(kQqR)
(b) Now assume that the positively charged sphere moves with speed V through a space which is filled with small particles of mass m and charge – q. The small particles are at rest and their number density is n [i.e., number of particles per unit volume of space is n].
The particles hit the sphere and stick to it. Calculate the rate at which the sphere starts losing its positive charge dQdt. Express your answer in terms of b0
View SolutionPositive charge Q is distributed uniformly over a circular ring of radius R. A particle having a mass m and a negative charge q, is placed on its axis at a distance x from the centre. Find the force on the particle. Assuming x ltltR, find the time period of oscillation of the particle if it is released from there.
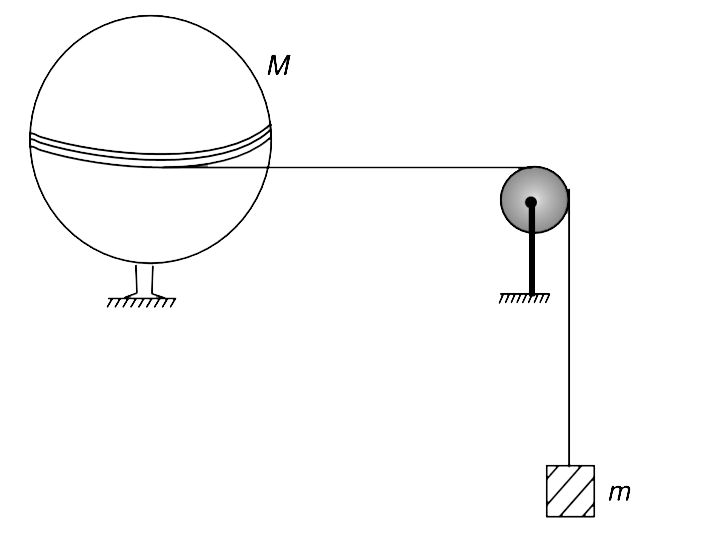
View SolutionA solid uniform sphere of mass M and radius R can rotate about a fixed vertical axis. There is no frictional torque acting at the axis of rotation. A light string is wrapped around the equator of the sphere. The string has exactly 6 turns on the sphere. The string passes over a light pulley and carries a small mass m at its end (see figure). The string between the sphere and the pulley is always horizontal. The system is released from rest and the small mass falls down vertically. The string does not slip on the sphere till 5 turns get unwound. As soon as 5th turn gets unwound completely, the friction between the sphere and the string vanishes all of a sudden.
(a) Find the angular speed of the sphere as the string leaves it.
(b) Find the change in acceleration of the small mass m after 5 turns get unwound from the sphere.
View SolutionA ring of radius R having total charge Q uniformly distributed over the ring has a charge particle q kept at its centre. If a transverse pulse is created on the ring, then find the time when pulse completes one revolution.(Total mass of ring is m)
View Solution
