A particle of mass 220meV/c2 collides with a hydrogen tom at rest. Soon after the collisionthe particle comes to rest, and the atom recoils and goes to its first excited state. The initial kinetic energy of the particle (in eV) is N4. The value of N is :
(Given the mass of the hydrogen atom to be 1GeV/c2)_____________
To solve the problem step by step, we will analyze the collision of the particle with the hydrogen atom and apply the principles of conservation of momentum and energy.
Step 1: Identify the masses involved
- Mass of the particle, mp=220MeV/c2=220×106eV/c2
- Mass of the hydrogen atom, mH=1GeV/c2=109eV/c2
Step 2: Calculate the ratio of the masses
To find the ratio of the mass of the hydrogen atom to the mass of the particle:
mHmp=109220×106=1092.2×108=1000220≈4.54
Thus, we can express the mass of hydrogen in terms of the mass of the particle:
mH≈4.54mp
Step 3: Apply conservation of momentum
Before the collision, the particle has momentum mv (where m is the mass of the particle and v is its velocity), and the hydrogen atom is at rest. After the collision, the particle comes to rest, and the hydrogen atom recoils with velocity v1. By conservation of momentum:
mv=mHv1
Substituting mH:
mv=4.54mpv1
Cancelling mp from both sides:
v=4.54v1⇒v1=v4.54
Step 4: Calculate the initial and final kinetic energies
The initial kinetic energy KEi of the particle is given by:
KEi=12mpv2
The final kinetic energy KEf of the hydrogen atom is:
KEf=12mHv21=12(4.54mp)(v4.54)2=12(4.54mp)v2(4.54)2=mpv22⋅4.54
Step 5: Calculate the energy transferred to the hydrogen atom
The energy transferred to the hydrogen atom is the difference in kinetic energy:
ΔKE=KEi−KEf=12mpv2−mpv22⋅4.54
Factoring out 12mpv2:
ΔKE=12mpv2(1−14.54)=12mpv2(4.54−14.54)=12mpv2(3.544.54)
Step 6: Relate the energy transferred to the excited state of hydrogen
The energy required to excite the hydrogen atom to its first excited state is given as 10.2eV:
ΔKE=10.2eV
Substituting the expression for ΔKE:
12mpv2(3.544.54)=10.2
Step 7: Find the initial kinetic energy in terms of N
The initial kinetic energy is given as N4:
KEi=N4=12mpv2
Thus, we can relate N4 to the previous equations:
N4=12mpv2
From this, we can express v2:
v2=N2mp
Step 8: Substitute v2 back into the energy equation
Substituting v2 into the energy transferred equation:
12mp(N2mp)(3.544.54)=10.2
This simplifies to:
N⋅3.548.54=10.2
Solving for N:
N=10.2⋅8.543.54≈51
Final Answer
The value of N is 51.
---
- Mass of the particle, mp=220MeV/c2=220×106eV/c2
- Mass of the hydrogen atom, mH=1GeV/c2=109eV/c2
To find the ratio of the mass of the hydrogen atom to the mass of the particle:
mHmp=109220×106=1092.2×108=1000220≈4.54
Thus, we can express the mass of hydrogen in terms of the mass of the particle:
mH≈4.54mp
Before the collision, the particle has momentum mv (where m is the mass of the particle and v is its velocity), and the hydrogen atom is at rest. After the collision, the particle comes to rest, and the hydrogen atom recoils with velocity v1. By conservation of momentum:
mv=mHv1
Substituting mH:
mv=4.54mpv1
Cancelling mp from both sides:
v=4.54v1⇒v1=v4.54
The initial kinetic energy KEi of the particle is given by:
KEi=12mpv2
The final kinetic energy KEf of the hydrogen atom is:
KEf=12mHv21=12(4.54mp)(v4.54)2=12(4.54mp)v2(4.54)2=mpv22⋅4.54
The energy transferred to the hydrogen atom is the difference in kinetic energy:
ΔKE=KEi−KEf=12mpv2−mpv22⋅4.54
Factoring out 12mpv2:
ΔKE=12mpv2(1−14.54)=12mpv2(4.54−14.54)=12mpv2(3.544.54)
The energy required to excite the hydrogen atom to its first excited state is given as 10.2eV:
ΔKE=10.2eV
Substituting the expression for ΔKE:
12mpv2(3.544.54)=10.2
The initial kinetic energy is given as N4:
KEi=N4=12mpv2
Thus, we can relate N4 to the previous equations:
N4=12mpv2
From this, we can express v2:
v2=N2mp
Substituting v2 into the energy transferred equation:
12mp(N2mp)(3.544.54)=10.2
This simplifies to:
N⋅3.548.54=10.2
Solving for N:
N=10.2⋅8.543.54≈51
The value of N is 51.
Topper's Solved these Questions
Similar Questions
A particle of mass m is moving along the x-axis with initial velocity u i . It collides elastically with a particle of mass 10 m at rest and then moves with half its initial kinetic energy (see figure).If sinθ1=√nsinθ2 then value of n is
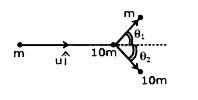
View SolutionA particle of mass 0.1kg moving with an initial speed v collides with another particle of same mass kept at rest. If after collision total energy becomes 0.2J . Then
View Solution
Knowledge Check
The total energy of an electron in the first excited state of hydrogen atom is about −3.4eV. Its kinetic energy in this state is
A−3.4eVB3.4eVC6.8eVD−6.8eVA nucleus of mass 220 amu in the free state decays to emit an α-particle . Kinetic energy of the α-particle emitted is 5.4 MeV. The recoil energy of the daughter nucleus is
A0.25 MeVB0.5 MeVC0.1 MeVD0.75 MeVA particle of mass m1 moving with velocity v collides with a mass m2 at rest, then they get embedded. Just after collision, velocity of the system
AincreasesBdecreasesCremains constantDbecomes zero
The value of 'n' of the highest excited state that an electron of hydrogen atom in the ground state can reach when 12.09eV energy is given to the hydrogen atom is.
View SolutionA particle of mass m starts from rest and moves in a circular path of radius R with a uniform angular acceleration α The kinetic energy of the particle after n revolutions is
View SolutionA particle of mass m1 makes a head - on elastic collision with another particle of mass m2 at rest. m1 rebounds straight back with 49 of its initial kinetic energy . Then m1m2 is :
View SolutionAn electron collides with a hydrogen atom in its ground state and excites it to n=3 ,. The energy gives to hydrogen atom n this inelastic collision is [Neglect the recoiling of hydrogen atom]
View SolutionThe energy of a hydrogen atom in its ground state is −13.6eV. The energy of the level corresponding to the quantum number n=2 (first excited state) in the hydrogen atom is
View Solution
