A spaceship in space sweeps stationary interplanetary dust . As a result , its mass increase at a rate dM(t)dt=bv2(t) , where v(t) is its instantaneous velocity . The instantaneous acceleration of the satellite is :
−bv3(t)
−bv3M(t)
−2bv3M(t)
−bv32M(t)
To solve the problem, we need to find the instantaneous acceleration of the spaceship as it sweeps up interplanetary dust. We are given that the mass of the spaceship increases at a rate given by:
dM(t)dt=bv2(t)
where v(t) is the instantaneous velocity of the spaceship.
1. Understanding the Problem:
We know that the spaceship is gaining mass as it collects dust. This mass gain affects its acceleration. According to Newton's second law, the force acting on an object is equal to the rate of change of momentum.
2. Using Newton's Second Law:
The force F can be expressed as:
F=dpdt=d(mv)dt
where p is the momentum.
3. Applying the Product Rule:
Since both mass m and velocity v are functions of time, we apply the product rule:
d(mv)dt=mdvdt+vdmdt
4. Setting Up the Equation:
According to Newton's second law, the force can also be expressed as:
F=mdvdt+vdmdt
Since the spaceship is not experiencing any external force (ignoring thrust), we can set this equal to zero:
0=mdvdt+vdmdt
5. Rearranging the Equation:
Rearranging gives us:
mdvdt=−vdmdt
6. Substituting dmdt:
We substitute dmdt=bv2 into the equation:
mdvdt=−v(bv2)
Simplifying this, we get:
mdvdt=−bv3
7. Finding Acceleration:
Now, we can solve for acceleration a=dvdt:
dvdt=−bv3m
Thus, the instantaneous acceleration a of the spaceship is:
a=−bv3m
Final Answer:
The instantaneous acceleration of the spaceship is given by:
a=−bv3m
We know that the spaceship is gaining mass as it collects dust. This mass gain affects its acceleration. According to Newton's second law, the force acting on an object is equal to the rate of change of momentum.
The force F can be expressed as:
F=dpdt=d(mv)dt
where p is the momentum.
Since both mass m and velocity v are functions of time, we apply the product rule:
d(mv)dt=mdvdt+vdmdt
According to Newton's second law, the force can also be expressed as:
F=mdvdt+vdmdt
Since the spaceship is not experiencing any external force (ignoring thrust), we can set this equal to zero:
0=mdvdt+vdmdt
Rearranging gives us:
mdvdt=−vdmdt
We substitute dmdt=bv2 into the equation:
mdvdt=−v(bv2)
Simplifying this, we get:
mdvdt=−bv3
Now, we can solve for acceleration a=dvdt:
dvdt=−bv3m
Thus, the instantaneous acceleration a of the spaceship is:
a=−bv3m
The instantaneous acceleration of the spaceship is given by:
a=−bv3m
Topper's Solved these Questions
Similar Questions
A satellite in force-free sweeps stationary interplanetary dust at a rate of dMdt=αv, where M is mass and v is the speed of satellite and α is a constant. The tangential acceleration of satellite is
View SolutionThe velocity of a particle at an instant "t" is v=u+at ,where u is initial velocity and a is constant acceleration.The v -t graph are
View Solution
Knowledge Check
A satellite in a force - free space sweeps stationary interplanetary dust at a rate dM/dt=αv, where M is the mass , vis the velocity of the satellite and α is a constant. What is the deacceleration of the satellite ?
A−2αv2/MB−αv2/MC+αv2/MD−αv2A satellite in a force-free space sweeps stationary interplantary dust at a rate dMdt=βυ, where υ is the speed of escaping dust w.r.t. satellite and M is the mass of saetllite at that instant. The acceleration of satellite is
A−βυ2B−βυ2/2MC−βυ2/MD−Mβ/υ2A satellite in force free space sweeps stationary interplanetary dust at a rate of dM/dt=αv, where M is mass and v is the speed of satellite and α is a constant. The acceleration of satellite is
A−αv22MB−αv2C−2αv2MD−αv2M
A satellite in a force - free space sweeps stationary interplanetary dust at a rate dM/dt=αv, where M is the mass , vis the velocity of the satellite and α is a constant. What is the deacceleration of the satellite ?
View SolutionThe displacement of a particle is given by y=(6t2+3t+4)m, where t is in seconds. Calculate the instantaneous speed of the particle.
View SolutionThe diagram shows variation of 1v with respect to time (where v is in m/s).
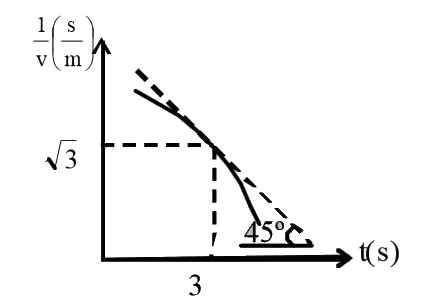
What is the instantaneous acceleration of body at t=3 sec. (inms2).
View SolutionThe velocity ofacar travelling on a straight road is given by the equation v=6+8t−t2 where vis in meters per second and t in seconds. The instantaneous acceleration when t=4.5s is :
View SolutionIn which of the following velocity (v) - time (t) graphs, the instantaneous acceleration decreases with time?
View Solution
