Which of the distance option(s) can be connect for a moving particle here, s is displacement, a is acceleration, and v is velocity
a = 0, s = 0
a≠0,v=0
a≠0,s=0
s≠0,v=0
The correct Answer is:A, B, C, D
To solve the question regarding the possible connections between displacement (s), acceleration (a), and velocity (v) for a moving particle, we will analyze each option step by step.
1. Understanding the Variables:
- Displacement (s): The change in position of the particle.
- Velocity (v): The rate of change of displacement.
- Acceleration (a): The rate of change of velocity.
2. Analyzing Each Option:
- Option 1: Acceleration (a) = 0 and Displacement (s) = 0.
- This scenario can occur when a particle is at rest at the origin (starting point). For example, if a particle has not moved from its initial position, both its displacement and acceleration can be zero.
- Conclusion: This option is possible.
- Option 2: Acceleration (a) ≠ 0 and Velocity (v) = 0.
- This can happen at the maximum height of a projectile. When an object is thrown upwards, at the peak, its velocity becomes zero, but the acceleration due to gravity (downward) is still acting on it (a = -g).
- Conclusion: This option is also possible.
- Option 3: Acceleration (a) = 0 and Displacement (s) = 0.
- This scenario can also occur when a particle is at rest at the origin. If the particle is not moving and there are no forces acting on it, both acceleration and displacement can be zero.
- Conclusion: This option is possible.
- Option 4: Displacement (s) ≠ 0 and Velocity (v) = 0.
- This situation can occur when a particle reaches the highest point in its upward motion. At this point, it has moved to a certain height (displacement is not zero), but its velocity is zero momentarily before it starts descending.
- Conclusion: This option is also possible.
3. Final Conclusion:
- All options (1, 2, 3, and 4) are possible for a moving particle.
Summary of Possible Connections:
- Option 1: a = 0, s = 0 → Possible
- Option 2: a ≠ 0, v = 0 → Possible
- Option 3: a = 0, s = 0 → Possible
- Option 4: s ≠ 0, v = 0 → Possible
- Displacement (s): The change in position of the particle.
- Velocity (v): The rate of change of displacement.
- Acceleration (a): The rate of change of velocity.
- Option 1: Acceleration (a) = 0 and Displacement (s) = 0.
- This scenario can occur when a particle is at rest at the origin (starting point). For example, if a particle has not moved from its initial position, both its displacement and acceleration can be zero.
- Conclusion: This option is possible.
- This can happen at the maximum height of a projectile. When an object is thrown upwards, at the peak, its velocity becomes zero, but the acceleration due to gravity (downward) is still acting on it (a = -g).
- Conclusion: This option is also possible.
- This scenario can also occur when a particle is at rest at the origin. If the particle is not moving and there are no forces acting on it, both acceleration and displacement can be zero.
- Conclusion: This option is possible.
- This situation can occur when a particle reaches the highest point in its upward motion. At this point, it has moved to a certain height (displacement is not zero), but its velocity is zero momentarily before it starts descending.
- Conclusion: This option is also possible.
- All options (1, 2, 3, and 4) are possible for a moving particle.
- Option 1: a = 0, s = 0 → Possible
- Option 2: a ≠ 0, v = 0 → Possible
- Option 3: a = 0, s = 0 → Possible
- Option 4: s ≠ 0, v = 0 → Possible
Topper's Solved these Questions
Similar Questions
Knowledge Check
If the displacement of a moving particle is given by s=5+20t−2t2, then acceleration when velocity is zero, is
A0B4 units/sec2C−4 units/sec2D−2 units/sec2For a particle moving along the vertical direction, assume s,v,a and t represent displacement, velocity, acceleration and time respectively. Assume the vertical upward direction as the positive direction.
 APQRS3241BPQRS1324CPQRS2134DPQRS4132
APQRS3241BPQRS1324CPQRS2134DPQRS4132For a particle moving in a straight line assume s,v,a and t represents displacement, velocity, acceleration and time respectively.
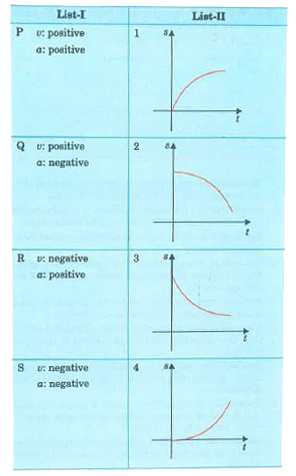 APQRS3241BPQRS1324CPQRS2134DPQRS4132
APQRS3241BPQRS1324CPQRS2134DPQRS4132
" If the velocity v of a particle varies as the square of its displacement "x" then the acceleration varies as "
View SolutionThe displacement 's' of a moving particle at a time H is given by s=5+20t-2t^(2) .Calculate its acceleration when the velocity is zero.
View SolutionThe acceleration (a) of a particle moving in a straight line varies with its displacement (S) as a=2S. The velocity of the particle is zero and zero displacement. Find the corresponding velocity-displacement equation.
View SolutionThe acceleration of a particle moving in a straight line varies with its displacement as,a=2s+1 veocity o particle is zero at zero displacement. Find the corresponding velocity - displacement equation.
View SolutionVelocity (v) versus displacement (s) graph of a particle moving in a straight line is shown in figure. Corresponding acceleration (a) versus velocity (v) graph will be
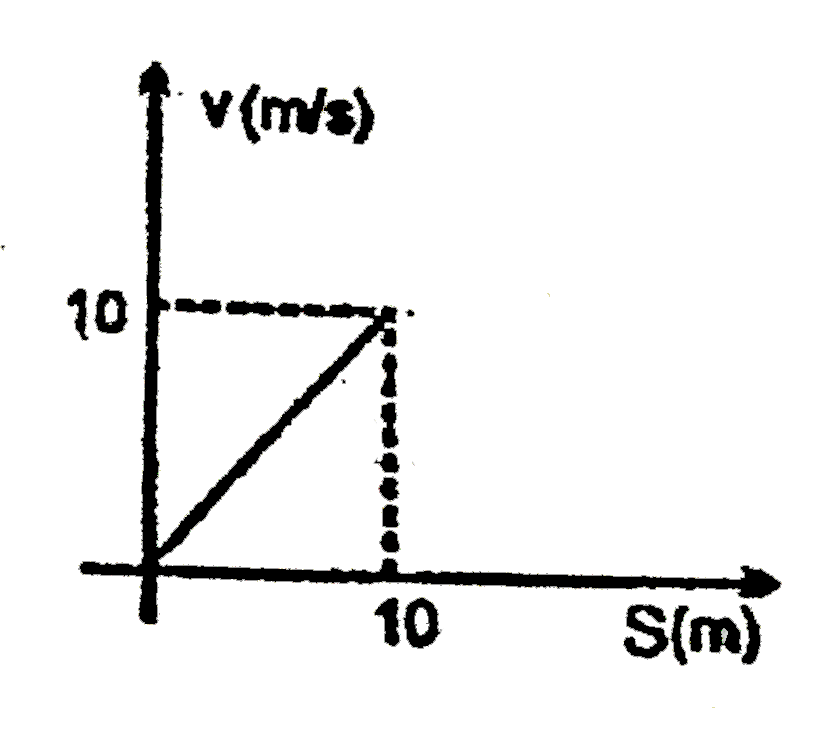
View Solution
