A rod of mass m and length l is sliding against a smooth vertical wall as shown. The speed of the bottom end of the rod at the instant shown is . The magnitude of angular momentum of the rod about ICR. (instantaneous axis of rotation) at the instant when is
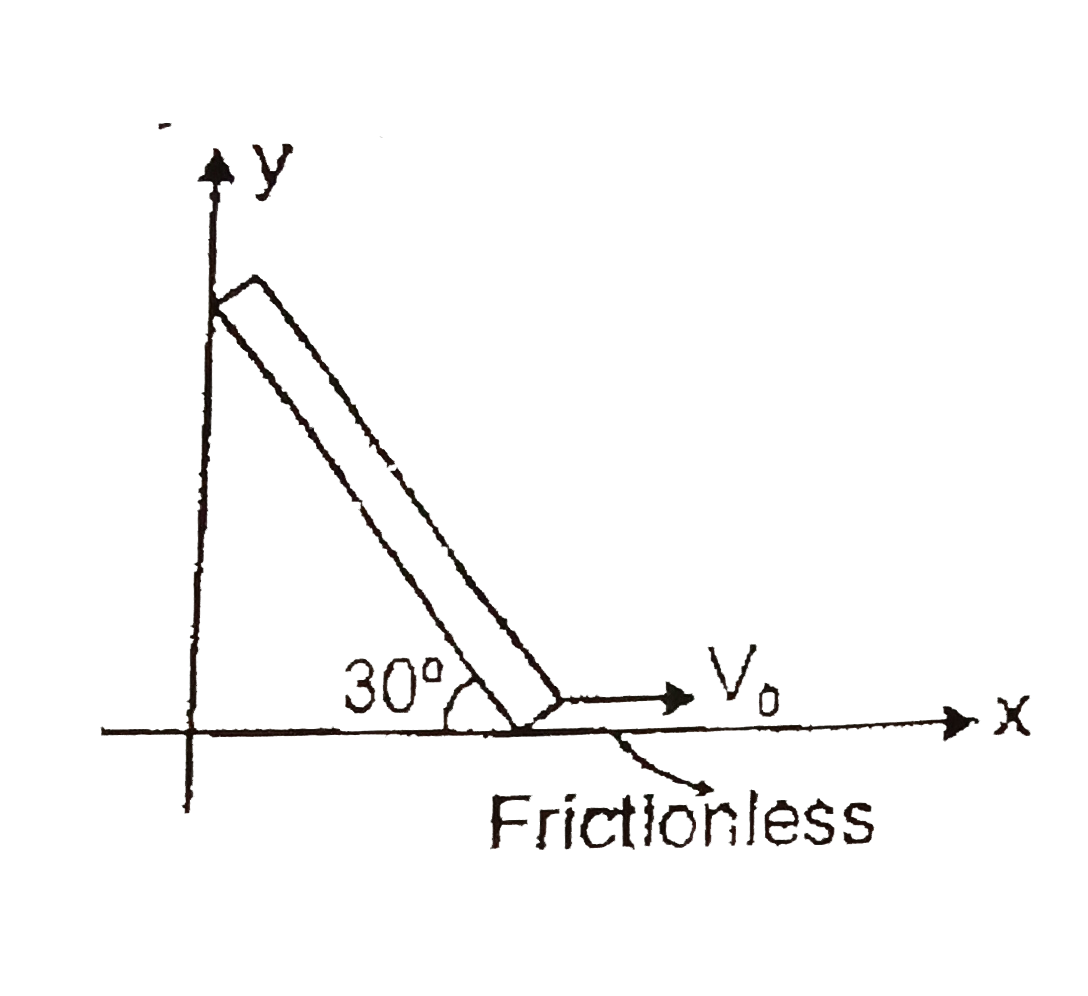
None of these
The correct Answer is:C
Calculating torque on upper disc (ring element)

Topper's Solved these Questions
Similar Questions
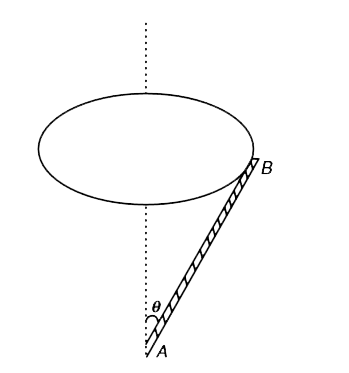
A uniform rod of mass m and length L is fixed to an axis, making an angle θ with it as shown in the figure. The rod is rotated about this axis so that the free end of the rod moves with a uniform speed ‘v’. Find the angular momentum of the rod about the axis. Is the angular momentum of the rod about point A constant?
View SolutionA uniform rod of mass 300 g and length 50 cm rotates at a uniform asngulr speed of 2 rad/s about an axis perpendicular to the rod through an end. Calculte a. the angular momentum of the rod about the axis of rotation b. the speed of thecentre of the rod and c. its kinetic energy.
View Solution
Knowledge Check
A rod AB of mass m and length l is rotating about a vertical axis as shown. It's moment of inertia about this axis is :
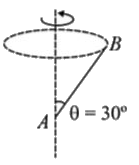 Aml23Bml24Cml216Dml212
Aml23Bml24Cml216Dml212A rod of length 1m is sliding in a corner as shown. At an instant when the rod makes an angle of 60∘ with the horizontal plane, the velocity of point A on the rod is 1 m/s. The angular velocity of the rod at this instant is :
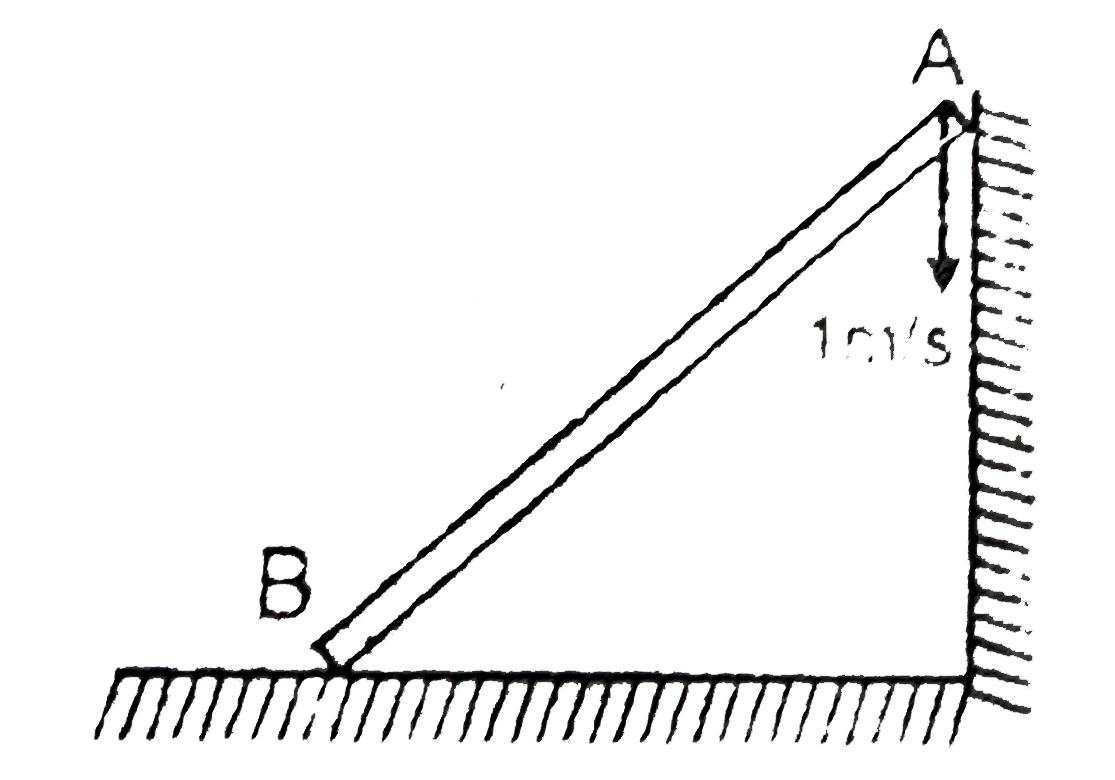 A2 rad/sB1.5 rad/sC0.5 rad/sD0.75 rad/s
A2 rad/sB1.5 rad/sC0.5 rad/sD0.75 rad/sIn the figure shown, the instantaneous speed of end A of the rod is v to the left. The angular velocity of the rod of length L must be
 Av2LBvLCv√32LDnone of these
Av2LBvLCv√32LDnone of these
A uniform thin rod of mass m and length l is standing on a smooth horizontal surface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View SolutionA uniform thin rod of mass m and length l is standing on a smooth horizontal suface. A slight disturbance causes the lower end to slip on the smooth surface and the rod starts falling. Find the velocity of centre of mass of the rod at the instant when it makes an angle θ with horizontal.
View Solution
A uniform rod of mass m is rotated about an axis passing through point O as shown. Find angular momentum of the rod about rotational law.
View SolutionA uniform rod of mass m and length l0 is rotating with a constant angular speed ω about a vertical axis passing through its point of suspension. Find the moment of inertia of the rod about the axis of rotation if it make an angle θ to the vertical (axis of rotation).
View SolutionA rod AB is placed on smooth inclined plane as shown in the figure. At the instant which is shown in the figure, the angular velocity of the rod is
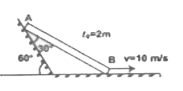
View Solution
