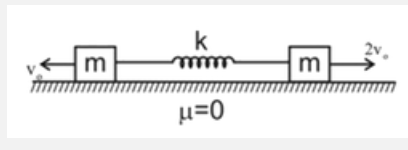
Two identical blocks of mass m, each are connected by a spring as shown in figure. At any instant of t = 0, one block is given a velocity V0 and other is given a velocity 2V0 in the same direction simultaneously as shown in figure. The maximum energy stored in spring
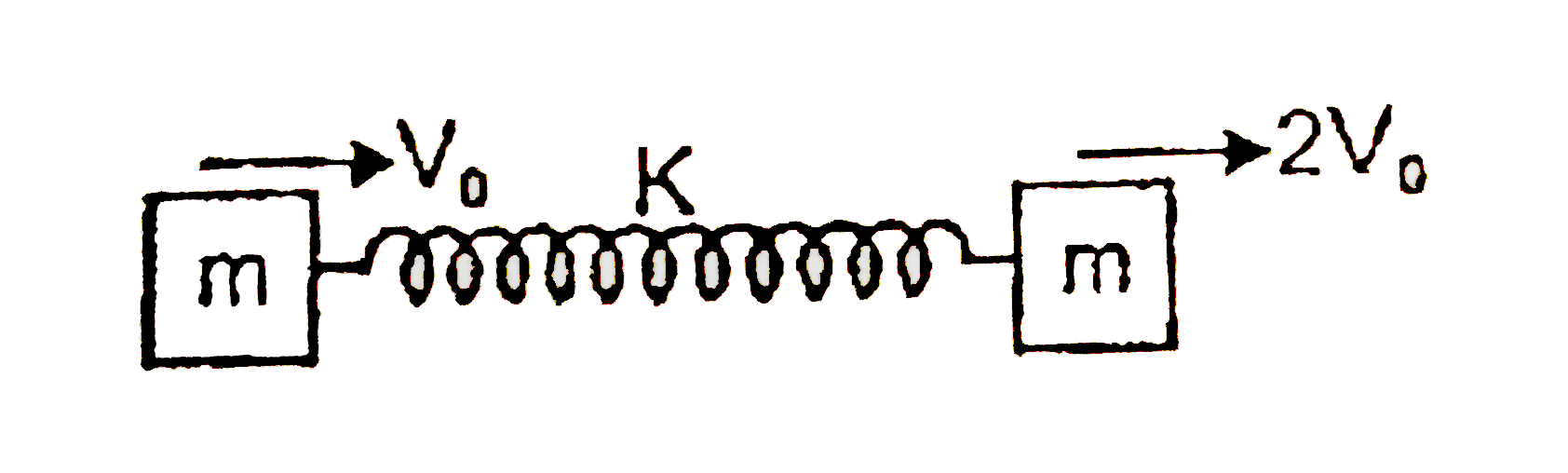
12mV20
14mV20
34mV20
52mV20
The correct Answer is:B
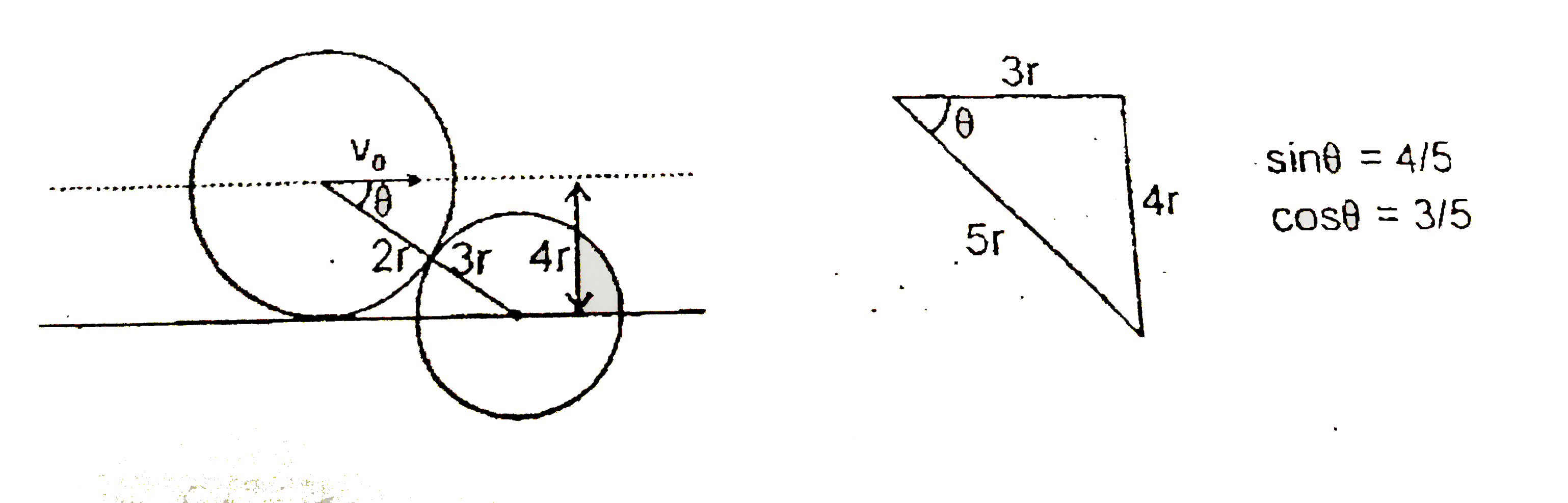
By conservation of linear momentum along line of impact.
∵ Both discs have same mass so velocities along line of impact are interchanged.
implies Velocity of bigger disc after collision =v0cosθ=v0(35)=3v05
Topper's Solved these Questions
Similar Questions
Two identical blocks of mass m, each are connected by a spring as shownin the figure. At any instant of time t=0, one block is given a velocity v1 and other is given a velocity v2(v1>v2) in the same direction simultaneously as shown in the figure. Find the maximum energy stored in the spring.
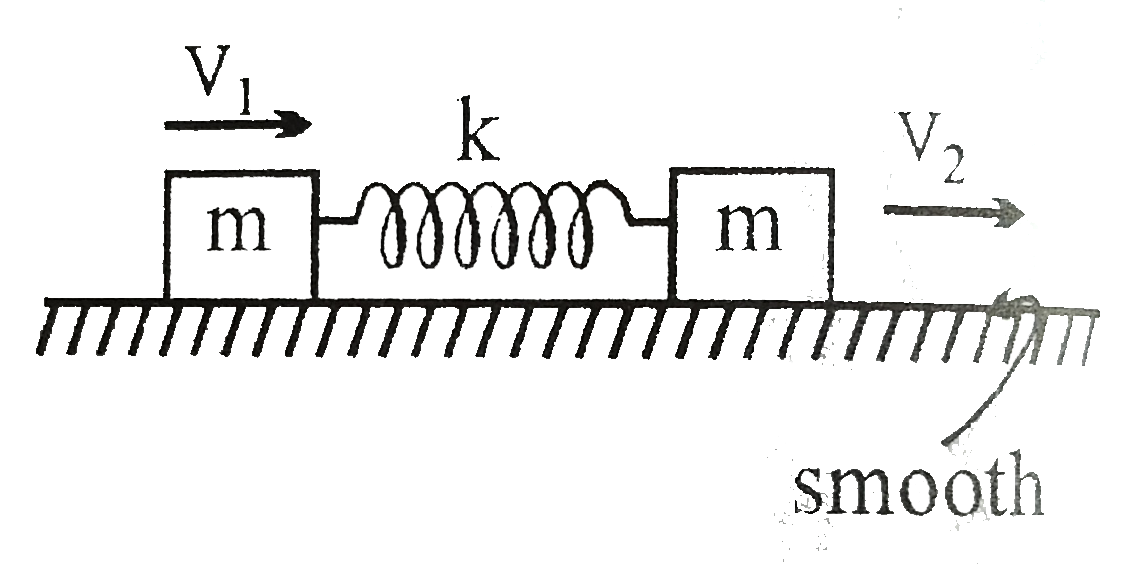 View Solution
View SolutionTwo masses are connected by a spring as shown in the figure. One of the masses was given velocity v = 2 k, as shown in figure where 'k' is the spring constant. Then maximum extension in the spring will be
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A block of mass m is suspended by different springs of force constant shown in figure.
 AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4
AT1=T2=T4BT1=T2andT3=T4CT1=T2=T3DT1=T3 and T2=T4 - Question 2 - Select One
Two identical blocks A and B of mass m joined together with a massless spring as shown in figure are placed on a smooth surface. If the block A moves with an acceleration a0, then the acceleration of the block B is
 Aa0B−a0CFm−a0DFm
Aa0B−a0CFm−a0DFm - Question 3 - Select One
Two masses A and B of mass M and 2M respectively are connected by a compressed ideal spring. The system in placed on a horizontal frictionless table and given a velocity uˆk in the z-direction as shown in the figure. The spring is then released. In the subsequent motion the line from B to A alwyas points along the ˆi unit vector. All some instant of time mass B has a x-component of velocity as vxˆi. The velocity →vA of mass A at that instant is :-
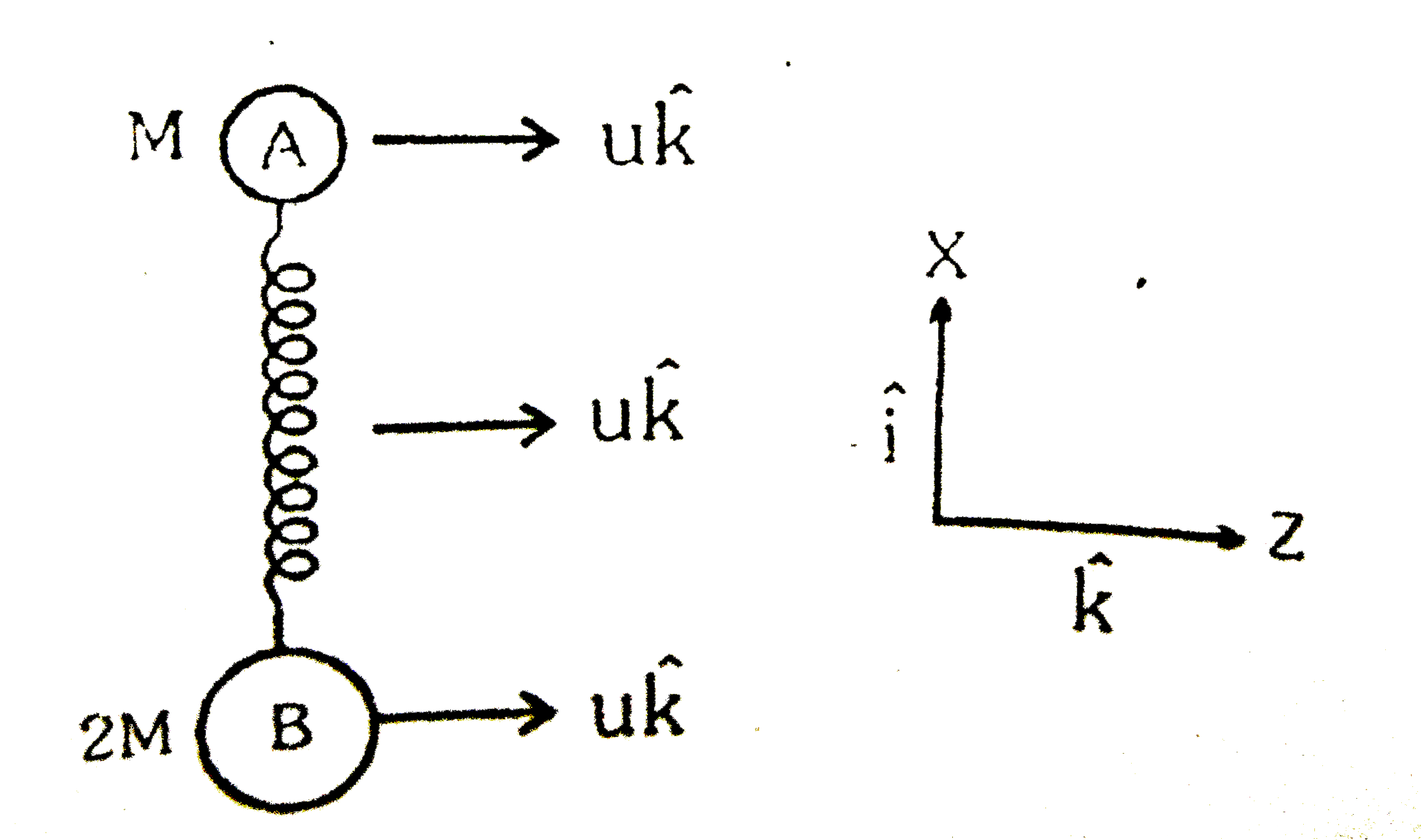 Avxˆi+uˆkB−vxˆi+uˆkC−2vxˆi+uˆkD2vxˆi+uˆk
Avxˆi+uˆkB−vxˆi+uˆkC−2vxˆi+uˆkD2vxˆi+uˆk

A block of mass 200 g is given velocity 2(m)/(s) on a horizontal surface as shown in the figure. Find the maximum compression of spring of spring constant k=100(N)/(m)View SolutionTwo blocks of masses m1andm2 are connected by a spring of spring constant k figure. The block of mass m2 is given a shapr imulse so that it acquires a velocity v0 twoards right. Find a. the velocity of the cenre of mas b. the maximum elongation that teh spring will suffer.
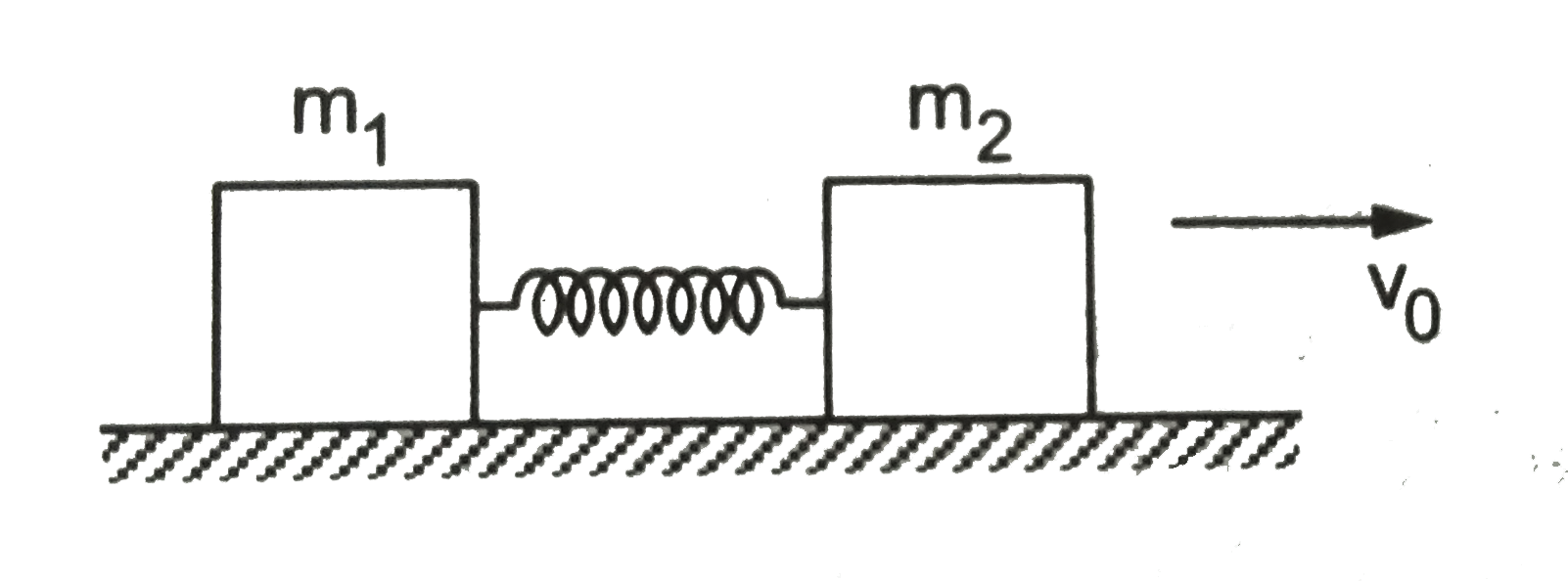 View Solution
View SolutionTwo ring of mass m and 2m are connected with a light spring and can slide over two frictionless parallel horizontal rails as shown in figure. Ring of mass m is given velocity 'v0' in horizontal direction as shown. Calculate the maximum stretch in spring during subsequent motion.
 View Solution
View SolutionThe figure shows two blocks of mass m each, connected by an ideal unstretched spring and then placed on a frictionless floor. If the blocks are given velocities v0and2v0 as shown, then the maximum extension in the spring is
 View Solution
View SolutionA block of mass m is connected to a spring of spring constant k as shown in figure. The frame in which the block is placed is given an acceleration a towards left. Neglect friction between the block and the frame walls. The maximum velocity of the block relative to the frame is
 View Solution
View Solution

