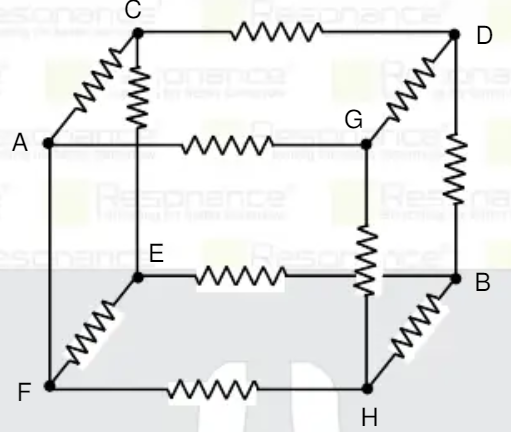
Figure (a) shows a cube made of 12 resistors each of resistance R. Find the equivalent resistance it the terminals A and B are connected to an emf source.
To find the equivalent resistance between terminals A and B of a cube made of 12 resistors, each of resistance R, we can follow these steps:
1. Understanding the Cube Configuration:
The cube has 12 edges, and each edge has a resistor of resistance R. When terminals A and B are connected to an EMF source, the current will flow through the resistors along the edges of the cube.
2. Symmetry of the Cube:
Due to the symmetry of the cube, the current entering the cube at terminal A will divide equally among the three edges connected to A. Thus, if the total current entering at A is I, then each of the three edges will carry a current of I3.
3. Current Distribution:
As the current flows through the cube, it will continue to split at various junctions. For example, at the next junction after the first split, the current will again divide equally among the available paths.
4. Analyzing One Path:
Let's analyze one of the paths from A to B. The current I3 will flow through one edge (say from A to a vertex), and then it will split again at the next junction. The current will further divide into two paths, with each path carrying I6.
5. Applying Kirchhoff's Voltage Law (KVL):
We can apply KVL to a loop that includes the resistors. For example, consider the loop A → 1 → 2 → 3 → 4 → B. The voltage across each resistor can be expressed as:
- From A to 1: I3R
- From 1 to 2: I6R
- From 2 to 3: I3R
- From 3 to B: 0 (no resistor)
Therefore, applying KVL gives:
V=I(13R+16R+13R)
6. Calculating the Total Voltage Drop:
Combine the terms:
V=I(26R+16R+26R)=I(56R)
7. Finding the Equivalent Resistance:
Since V=IReq, we can equate the two expressions:
Req=56R
Final Answer:
The equivalent resistance between terminals A and B is:
Req=56R
The cube has 12 edges, and each edge has a resistor of resistance R. When terminals A and B are connected to an EMF source, the current will flow through the resistors along the edges of the cube.
Due to the symmetry of the cube, the current entering the cube at terminal A will divide equally among the three edges connected to A. Thus, if the total current entering at A is I, then each of the three edges will carry a current of I3.
As the current flows through the cube, it will continue to split at various junctions. For example, at the next junction after the first split, the current will again divide equally among the available paths.
Let's analyze one of the paths from A to B. The current I3 will flow through one edge (say from A to a vertex), and then it will split again at the next junction. The current will further divide into two paths, with each path carrying I6.
We can apply KVL to a loop that includes the resistors. For example, consider the loop A → 1 → 2 → 3 → 4 → B. The voltage across each resistor can be expressed as:
- From A to 1: I3R
- From 1 to 2: I6R
- From 2 to 3: I3R
- From 3 to B: 0 (no resistor)
V=I(13R+16R+13R)
Combine the terms:
V=I(26R+16R+26R)=I(56R)
Since V=IReq, we can equate the two expressions:
Req=56R
The equivalent resistance between terminals A and B is:
Req=56R
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTECHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself
32 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTECHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
59 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTECHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTECHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Knowledge Check
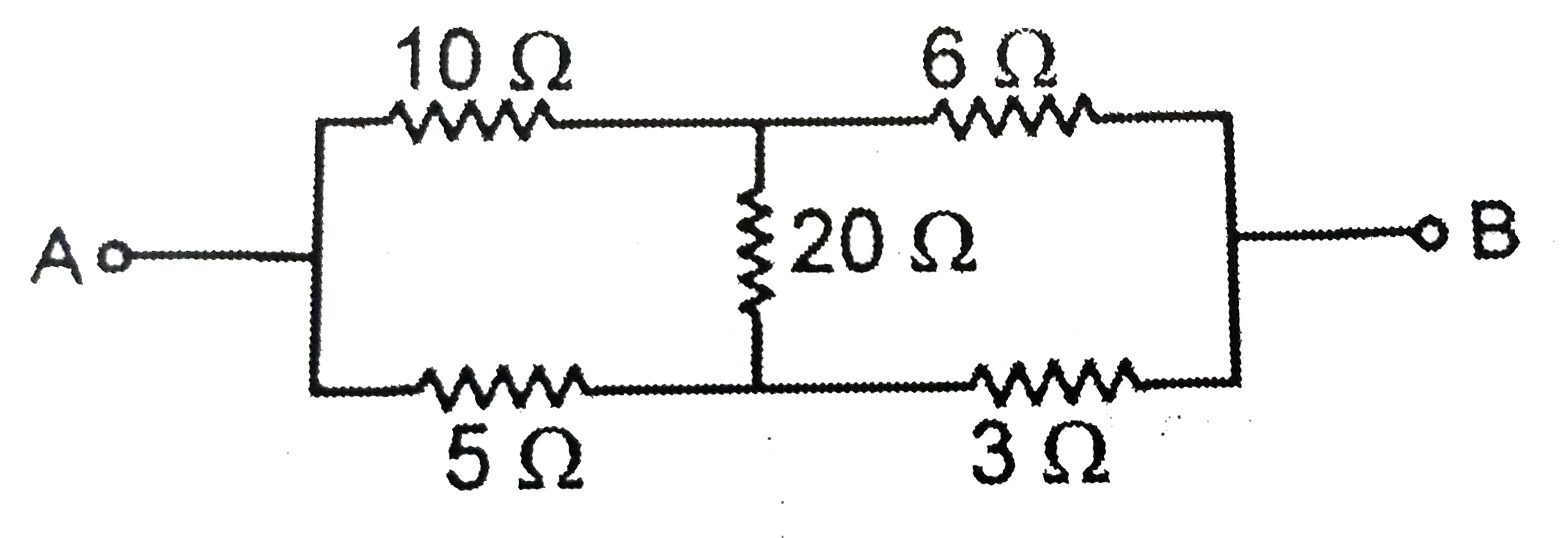
Each of the resistor shown in fig. has resistance R. Find the equivalent resistance between A and B
 A7R4B5R4C9R4D11R4
A7R4B5R4C9R4D11R4
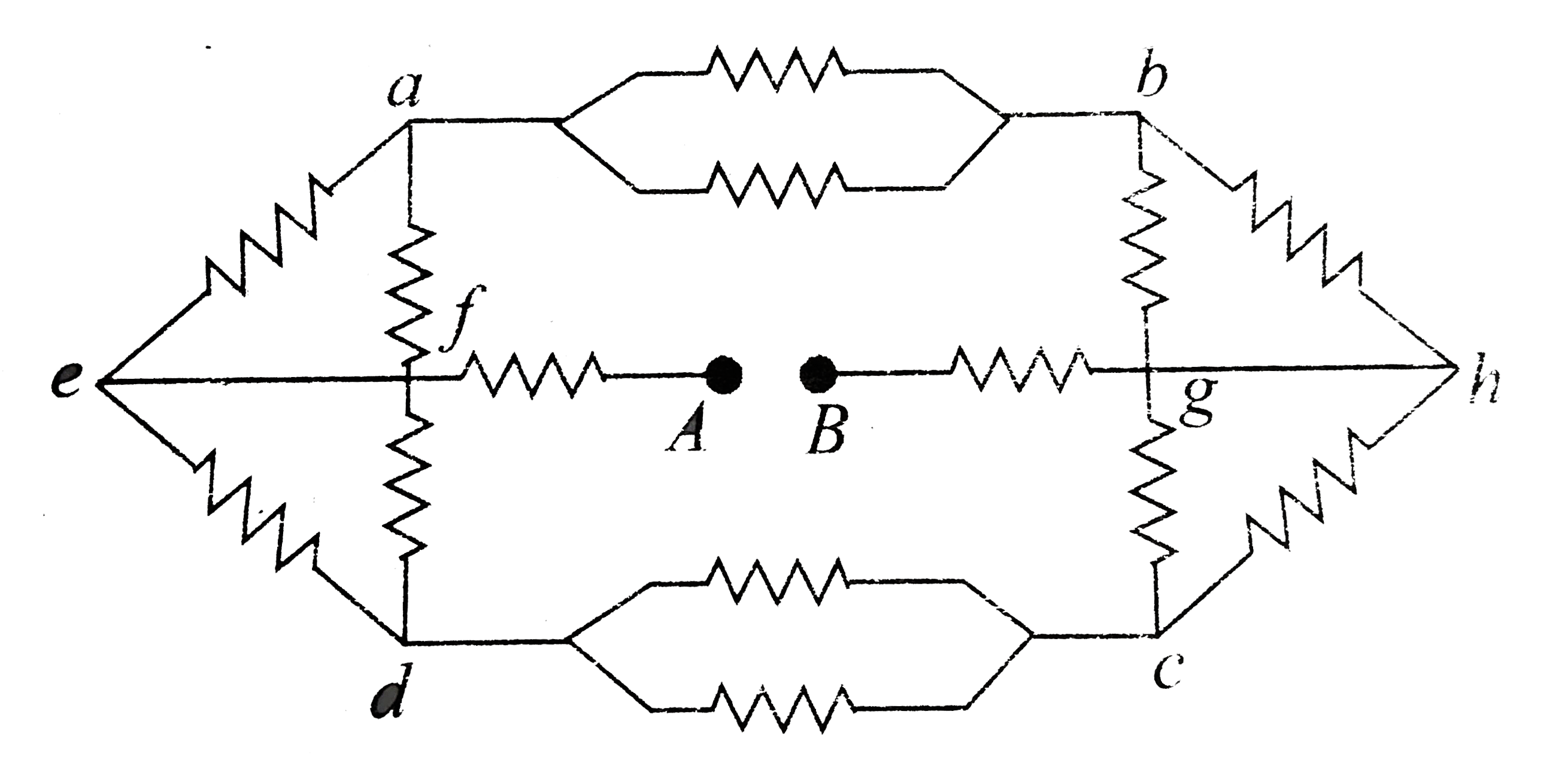
In the adjoining network of resistors each is of resistance rΩ. Find the equivalent resistance between A and B.
View SolutionA cube made up of wire each of resistance R. The find equivalent resistance across its diagnol
View SolutionFind the equivalent resistance between the terminal points A and B in the network shown in the figure.
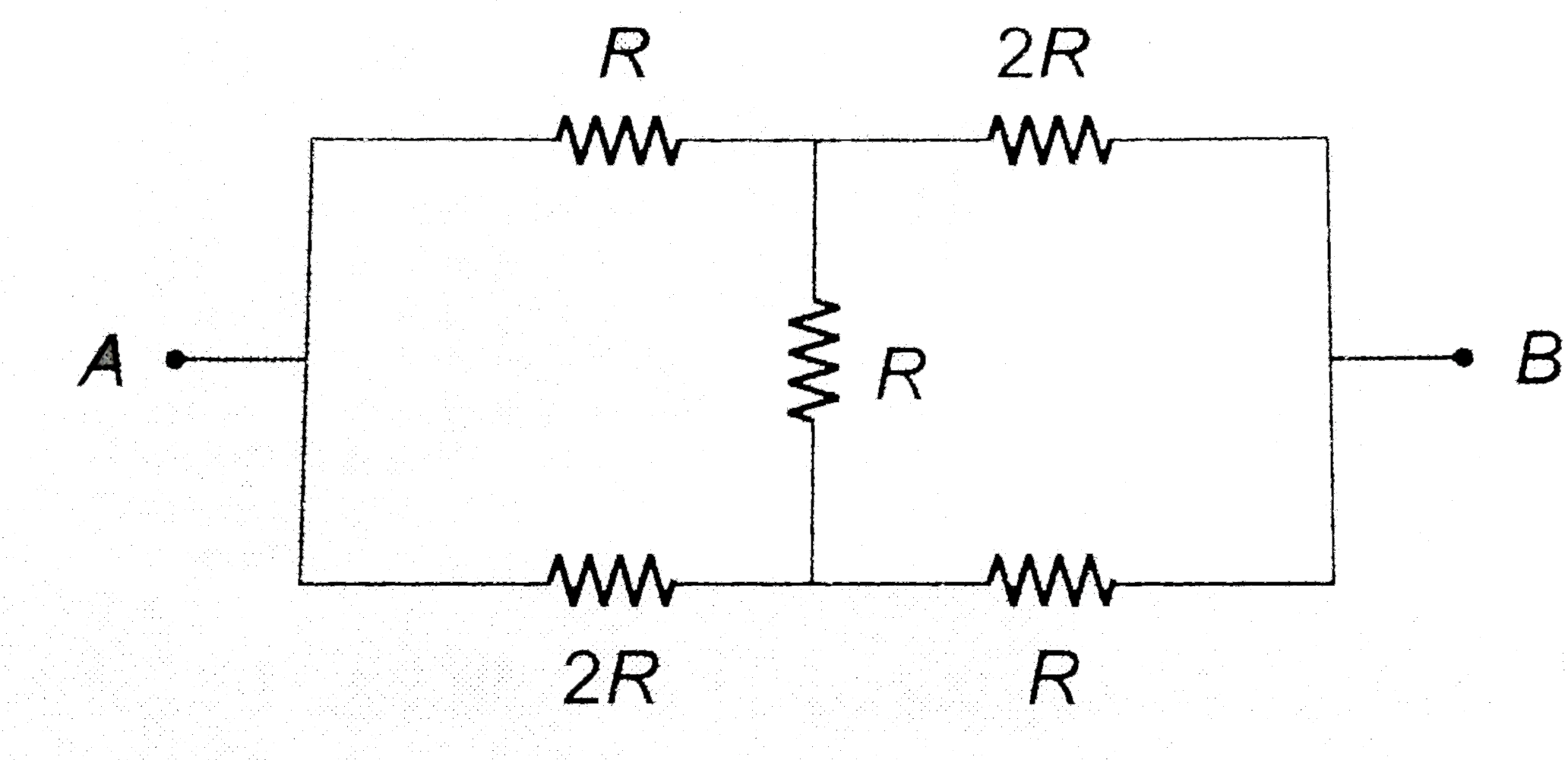 .
.
View SolutionFind equivalent resistance of the circuit between the terminals A and B.
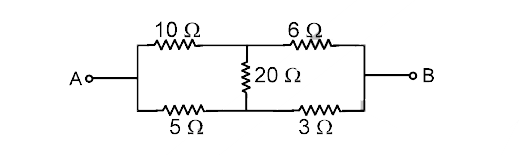
View SolutionFind equivalent resistance of the circuit between the terminals A and B.
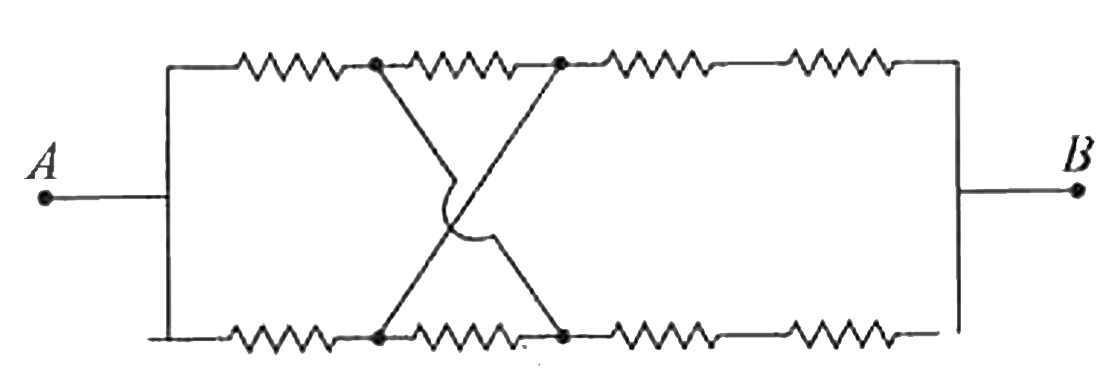
View SolutionFind the equivalent resistance between terminals A and B. Each resistor is of resistance R.
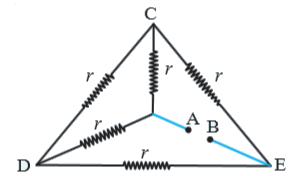
View SolutionIn the adjoining network of resistors, each is of resistance r ohm, the equivalent resistance between points A and B is–

View Solution