In the above question if a constant force F is applied on the rod. Find the velocity of the rod as a function of time assuming it started with zero initial velocity.

mdvdt=F−ilB….(1) i=BlvR+r……(2)
mdvdt=F−B2l2vR+r
let K=B2l2R+r⇒∫l0dVF−Kv=∫t0dtm
−[ln(F−KV)]v0=tm⇒ln(F−kVF)=−Ktm
F−KV=Fe−kt/m⇒V=FK(1−e−kt/m)
Similar Questions
in the above equation if a constant force F is applied on the rod.Find the velocity of the rod as a function of time assuming it started with zero initial velocity.
View SolutionA thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment, the end B starts experiencing constant force F which is always perpendicular to the original position of the stationary rod and directed in a horizontal plane. Find the angular velocity of the rod as a function of its rotation angle ϕ counted relative to the initial position.
View Solution
Knowledge Check
In the above question, find out the magnitude of net force exerted by the pulley on the rod R1:
A2FBFC2√2FDF√2A force F of constant magnitude acts on a block of mass 'm' and t=0,initially along positive x-direction. The direction of force F starts rotating with a constant angular velocity ω in anticlockwise sense. Then the magnitude of velocity of the block as a function of time 't' is ( initial block was at rest )
AFmωsin(ωt2)B2Fmωsin(ωt2)CF2mωsin(ωt2)D2F3mωsin(ωt2)
In the above question, find out the magnitude of net force exerted by the pulley on the rod R1:
View SolutionA uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.
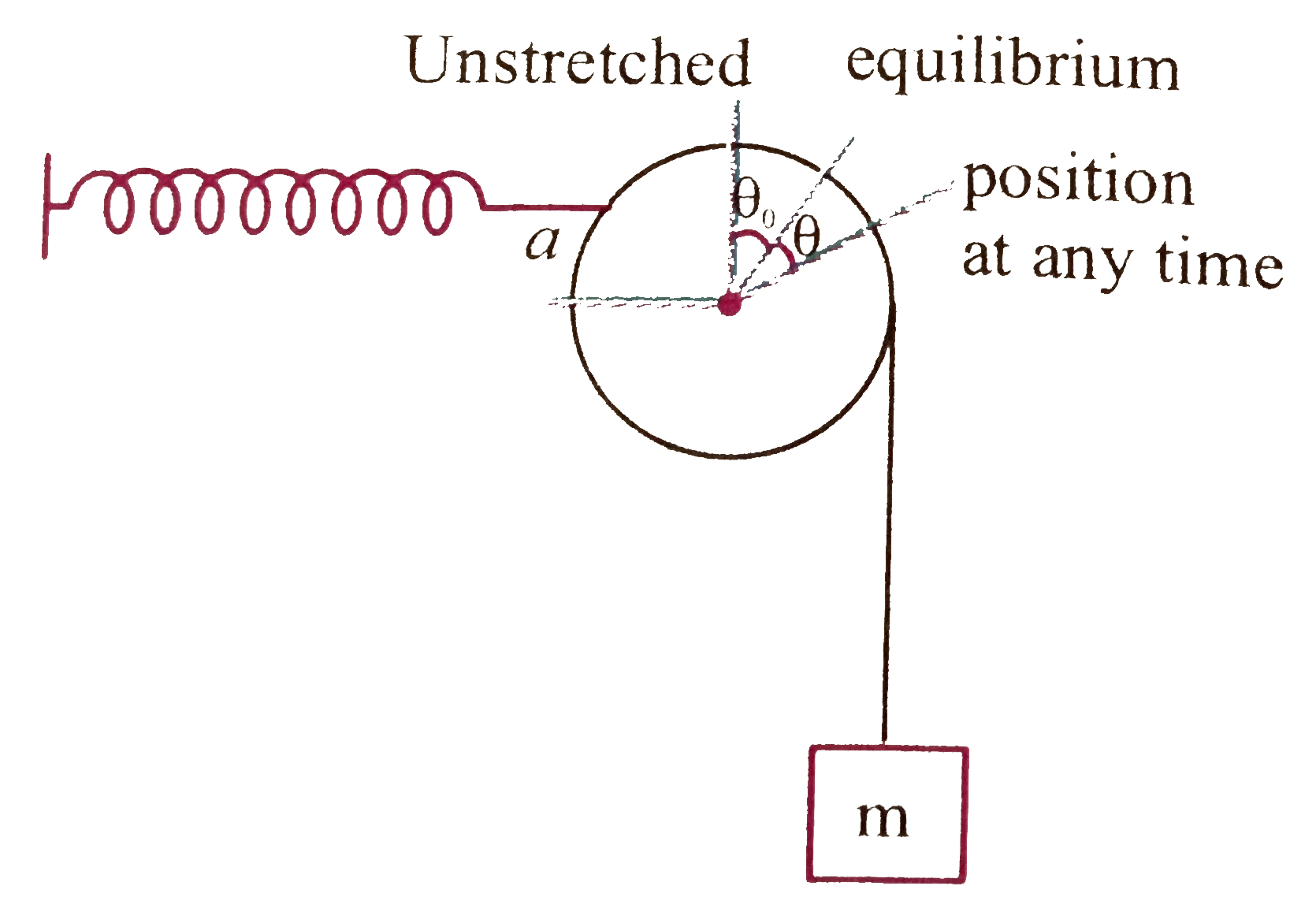
View SolutionA thin horizontal uniform rod AB of mass m and length l can rotate freely about a vertical axis passing through its end A. At a certain moment the end B starts experiencing a constant force F which is always perpendicular to the original position of the stationary rod and directed in a horizonatal plane. Find the angular velocity of the rod as a function of its rotation angle φ counted relative to the initial position.
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
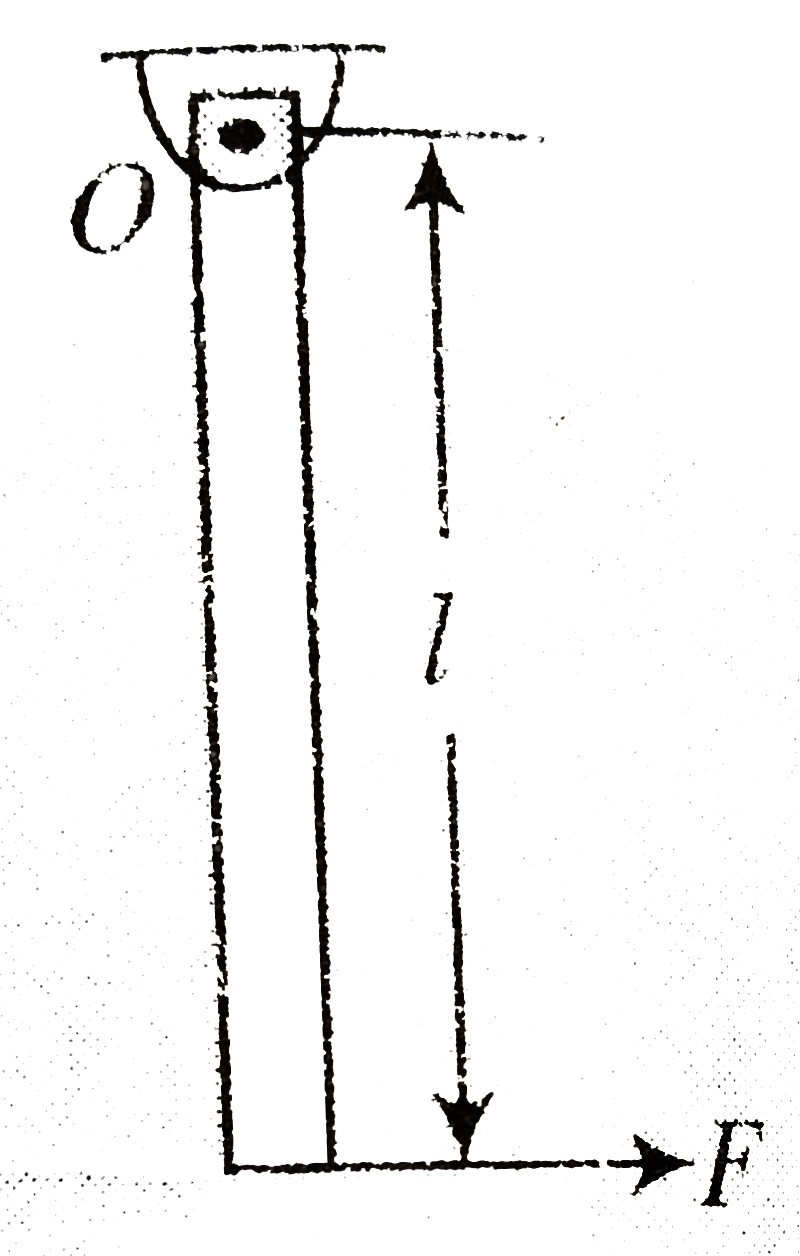
View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?
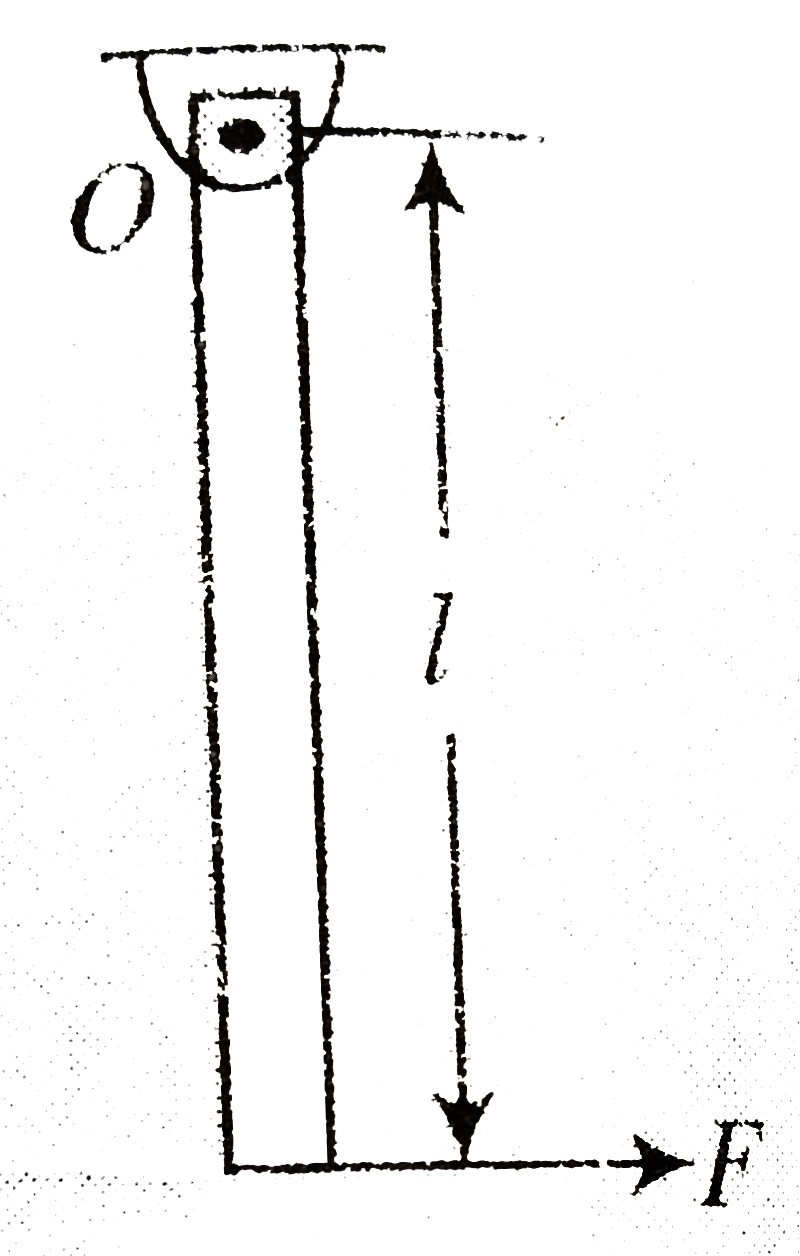
View SolutionA force F of constant magnitude acts on a block of mass 'm' and t=0,initially along positive x-direction. The direction of force F starts rotating with a constant angular velocity ω in anticlockwise sense. Then the magnitude of velocity of the block as a function of time 't' is ( initial block was at rest )
View Solution
