Find the velocity of the moving rod at time t if the initial velocity of the rod is v and a constant force F is applied on the rod.Neglect the resistance of the rod.

At any time t, let the velocity of the rod be v.
Applying Newtons law:F−ilB=ma ..(1)
Also Blv=i1,R=qc
Applying Kcl,
i=i1+dqdt=BlVR+ddt(BlvC)
or i=BlVR+BlCa
Putting the value of i in eq.(1), F−B2L2VR=(m+B2L2C)a=(m+B2L2C)dvdt
(m+B2L2C)dvF−B2L2VR=dt
Integrating both sides, and solving we get
v=FRB2l2(1−etB2l2R(m+CB2l2))

Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1
63 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1 PART 2
51 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- ELECTRODYNAMICSBOOK - RESONANCECHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - HLP
39 Videos
Similar Questions
Find the velocity of the moving rod at time t if the initial velocity of the rod is zero and a constant force F is applied on the rod.Neglect the resistance of the rod.

View SolutionA uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?

View Solution
Knowledge Check
Two long parallel metallic wires with a resistance 'R' from a horizontal plane . A conducting rod AB is on the wires shown in figure . The space has magnetic field pointing vertically downwards. The rod is given an initial velocity 'v0'. There is no friction in the wire and the rod . After a time 't' the velocity v of the rod will be such that :-
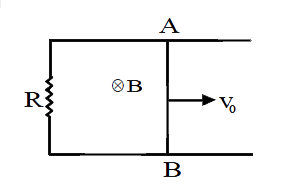 Av>v0Bv>v0Cv=v0Dv=−v0
Av>v0Bv>v0Cv=v0Dv=−v0
A uniform rod of mass m and length l is pivoted smoothly at O. A horizontal force acts at the bottom of the rod.
a. Find the angular velocity of the rod as the function of angle of rotation θ.
b.What is the maximum angular displacement of the rod?

View SolutionA uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.
View Solution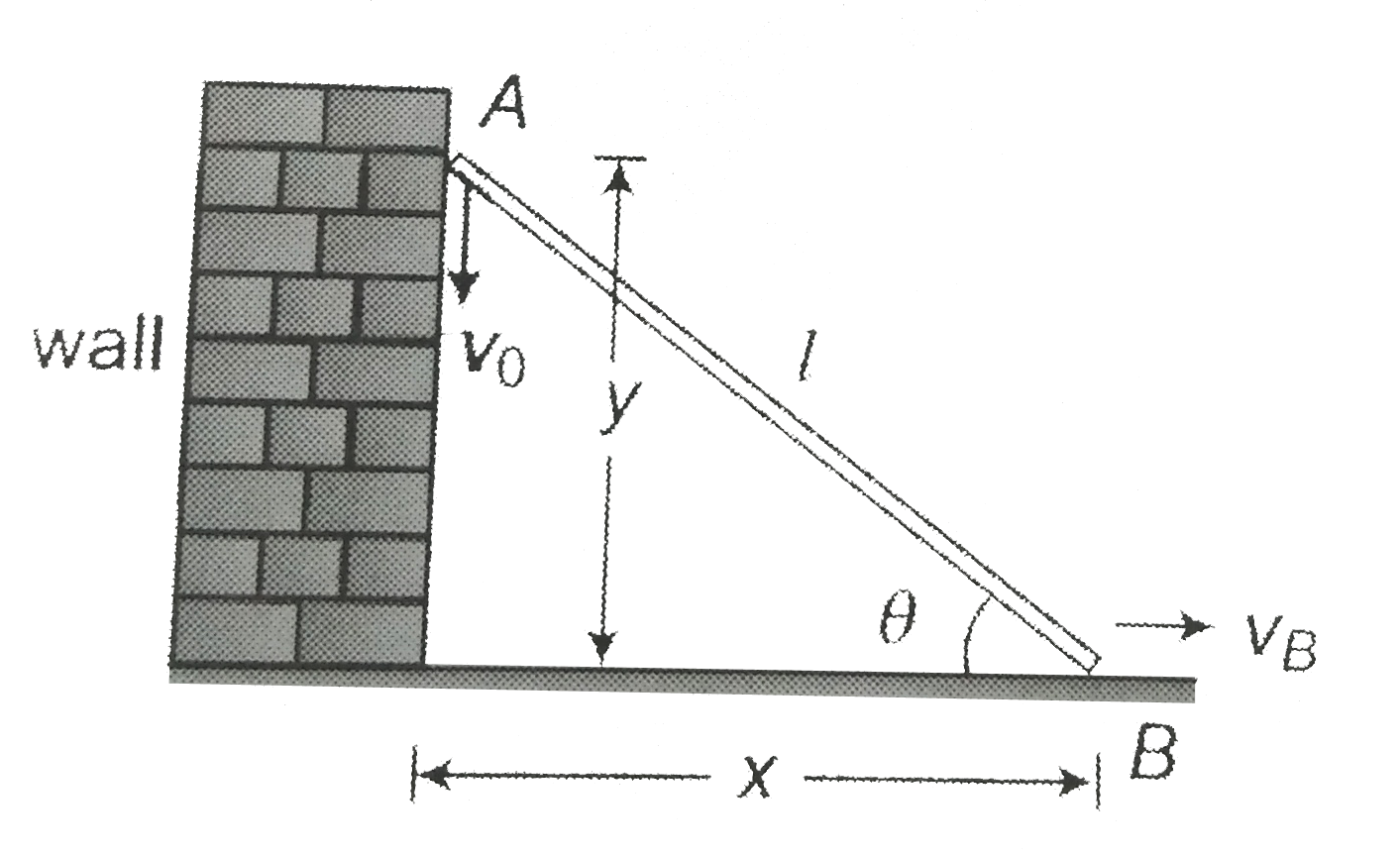
Consider a rod of length l resting on a wall and the floor. If the velocity of the upper end of a rod A is v0 in downward direction, find the velocity of the lower end B at this iinstant, when the rod makes an angle θ with horizontal
View SolutionA rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
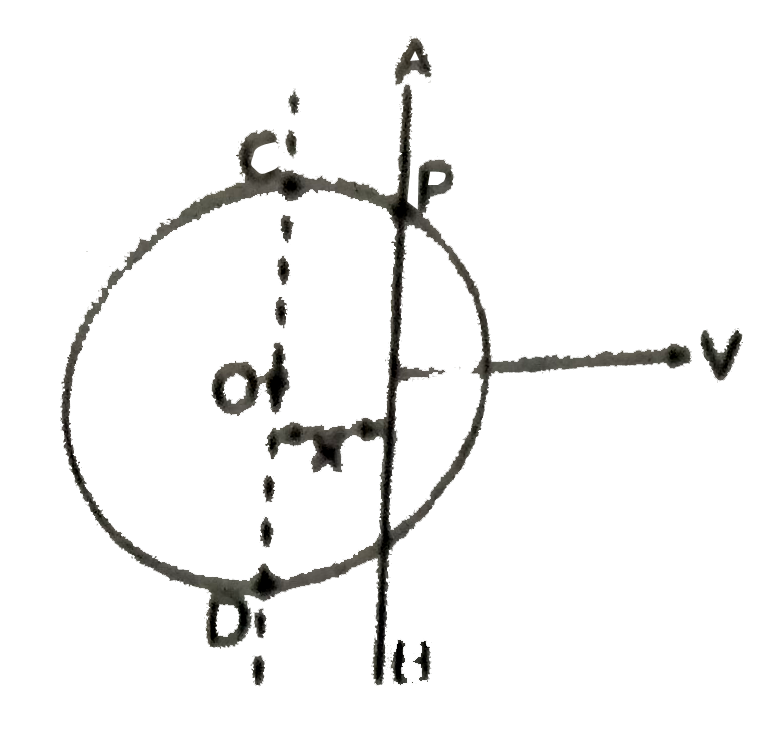
(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.
View SolutionA rod AB is moving on a fixed circle of radius R with constant velocity 'v' as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distance x=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.

(a) Find the speed of point of intersection P
(b) Find the angular speed of point of intersection
P with respect to centre of the circle.
View Solution
A rod AB is moving on a fixed circle of radius R with constant velocity v as shown in figure. P is the point of intersection of the rod and the circle. At an instant the rod is at a distancex=3R5 from centre of the circle. The velocity of the rod is perpendicular to the rod and the rod is always parallel to the diameter CD.
(i) Find the speed of point of intersection P.
(b) Find the angular speed of point of intersection P with respect to centre of the circle.
View SolutionA conducting circular loop of radius a and resistance per unit length R is moving with a constant velocity v0 , parallel to an infinite conducting wire carrying current i0. A conducting rod of length 2a is approaching the centre of the loop with a constant velocity v02 along the direction 2 of the current. At the instant t=0, the rod comes in contact with the loop at A and starts sliding on the loop with the constant velocity. Neglecting the resistance of the rod and the self-inductance of the circuit, find the following when the rod slides on the loop.

(a) The current through the rod when it is at a distance of (a2) from the point A of the loop.
(b) Force required to maintain the velocity of the rod at that instant.
View Solution
