Find out energy stored in an imaginary cubical volume of side a in front of a infinitely large non-conducting sheet of uniform charge density σ.
Energy stored : U=∫12ε0E2dV, where dV is small volume
∴U=12ε0E2∫dV ∵E is constant
∴U=12ε0σ24ε20.A3.=σ2a38ε0
Topper's Solved these Questions
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Problems
22 Videos
- ELECTROSTATICSBOOK - RESONANCECHAPTER - ELECTROSTATICSEXERCISE - Exercise-1 Section (A)
9 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCECHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - A.l.P
19 Videos
- EXPERIMENTAL PHYSICSBOOK - RESONANCECHAPTER - EXPERIMENTAL PHYSICSEXERCISE - PART -II
10 Videos
Similar Questions
A block having mass m and charge Q is resting on a frictionless plane at a distance d from fixed large non-conducting infinite sheet of uniform charge density −σ as shown in Figure. Assuming that collision of the block with the sheet is perfectly elastic, find the time period of oscillatory motion of the block. Is it SHM ?
View SolutionElectric field due to an infinite non-conducting sheet of surface charge density σ, at a distance r from it is
View Solution
Knowledge Check
A charged ball B hangs from a silk thread S, which makes an angle θ with a large charged conducting sheet P, as shown in figure. The surface charge density σ of the sheet is proportional to
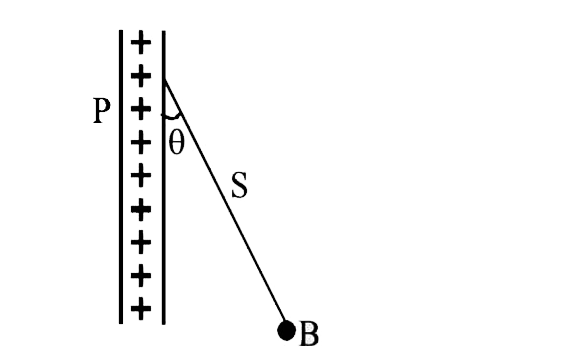A(a) cotθB(b) cosθC(c) tanθD(d) sinθ
Determine and draw the graph of electric field due to infinitely large non-conducting sheet of thickness t and uniform volume charge density ρ as a function of distance x from its symmetry plane.
(a) x<t2 (b) x≥t2
View SolutionA uniform rod AB of mass m and length l is hinged at its mid point C. The left half (AC) of the rod has linear charge density −λ and the right half (CB) has +λ where λ is constant. A large non conducting sheet of uniform surface charge density σ is also present near the rod. Initially the rod is kept perpendicular to the sheet. The end A of the rod is initialy at a distance d. Now the rod is rotated by a small angle in the plane of the paper and released. Prove that the rod will perform SHM and find its time period.
View SolutionRepeat the question if sphere is a hollow non-conducting sphere of radius R and has uniform surface charge density σ.
View SolutionA particle of mass M and negative charge q is thrown in a gravity free space with speedd u from the point A on the large non conducting charged sheet with surface charge density (sigma), as shown in figure, Find the maximum distance from A on sheet where the rparticle can strike .
View Solution(a) Use Gauss's theorem to find the electric field due to a uniformly charged infinitely
Iarge plane thin sheet with surface charge density.Σ
(b) An infinitely large thin plane sheet has a uniform surface charge density +σ. Obtain the
expression for the amount of work done in bringing a point charge q from infinity to a
point , distant r, in front of the charged plane sheet.
View SolutionFind the magnetic field energy in a cubical region of edge 'a' above a large current carrying sheet carrying a uniform linear current density I A/m.
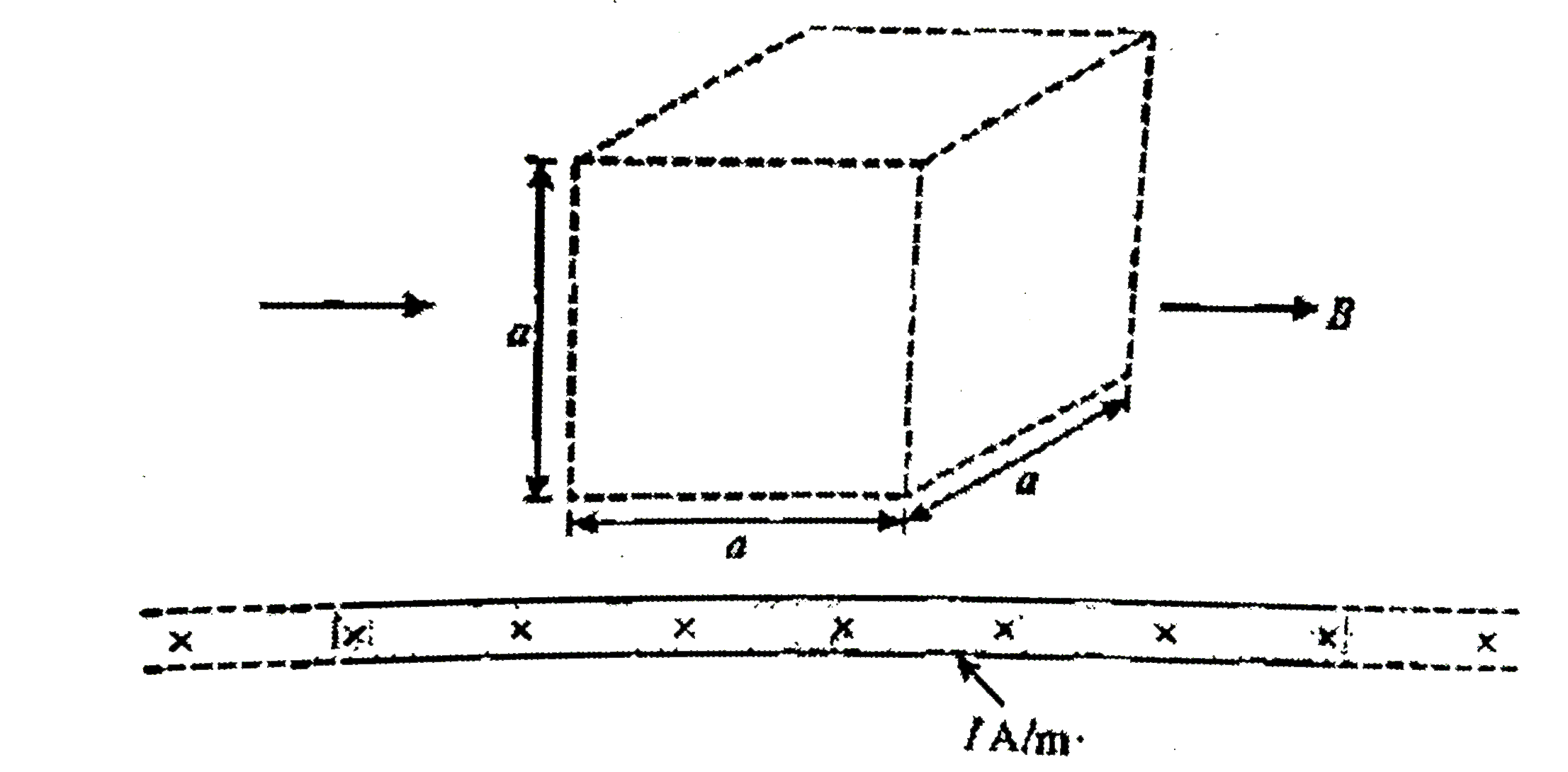
View SolutionIn a uniform electric field E if we consider an imaginary cubical closed surface of side a, then find the net flux through the cube ?
View Solution