Consider a force acting on a particle given as →F=yˆi+xˆj , where ( x, y ) is the instantaneous location of the particle. This type of force is :
Surely a conservation force
Surely a non-conservation force
Information insufficient to reach to a conclusion
Will be conservation only if the particle is constrained to move in the x-y plane.
The correct Answer is:A
Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION (II) : (SUBJECTIVE )
33 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION(II) : MCQ ( SINGLE CORRECT)
47 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS
3 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
Knowledge Check
Force acting on a particle is given by F=A−xBt, where x is in metre and t is in seconds. The dimensions of B is -
AMLT−2BM−1T−3CM−1TDMT−1A particle has initial velocity →v=3ˆi+4ˆj and a constant force →F=4ˆi−3ˆj acts on the particle. The path of the particle is :
Astraight lineBparabolicCcircularDellipticalA particle of mass 2kg moves under a force given by
→F=−(8N/m)(xˆi+yˆj)
where ˆi and ˆj are unit vectors in the x and y directions.
The particle is projected from the origin in xy plane with an initial velocity →v=(3m/s)ˆi+(4m/s)ˆj.
Select correct statement(s).ATime after which the particle will return to origin first timeis π/2 secBTime after which the particle will return to origin first time is π secCThe maximum disance between the particle and origin is 2mDThe maximum distance between the particle and origin is 2.5m
The velocity of a particle of mass 2 kg is given by →v=atˆi+bt2ˆj. Find the force acting on the particle.
View SolutionA particle of mass 'm' moves along the quarter section of the circular path whose centre is at the origin . The radius of the circular path is 'a'. A force →F=yˆi−xˆj newton acts on the particle, where x,y denote the coordinates of position of the particle. Calculate the work done by this force in taking, the particle from point, A(a,0) to point B(0,a) along the circular path.
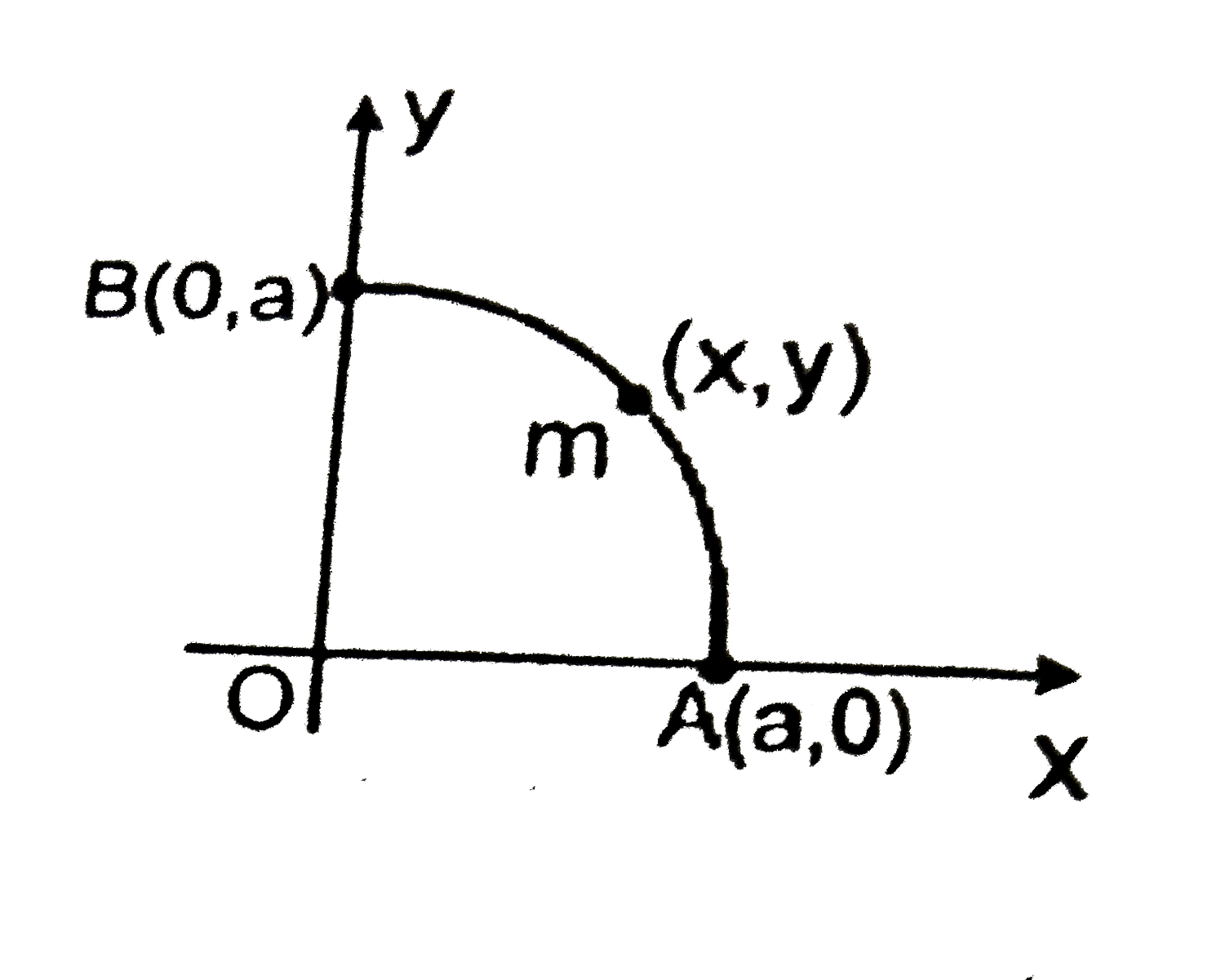
View SolutionA particle of mass 'm' moves along the quarter section of the circular path whose centre is at the origin . The radius of the circular path is 'a'. A force →F=yˆi−xˆj newton acts on the particle, where x,y denote the coordinates of position of the particle. Calculate the work done by this force in taking, the particle from point, A(a,0) to point B(0,a) along the circular path.
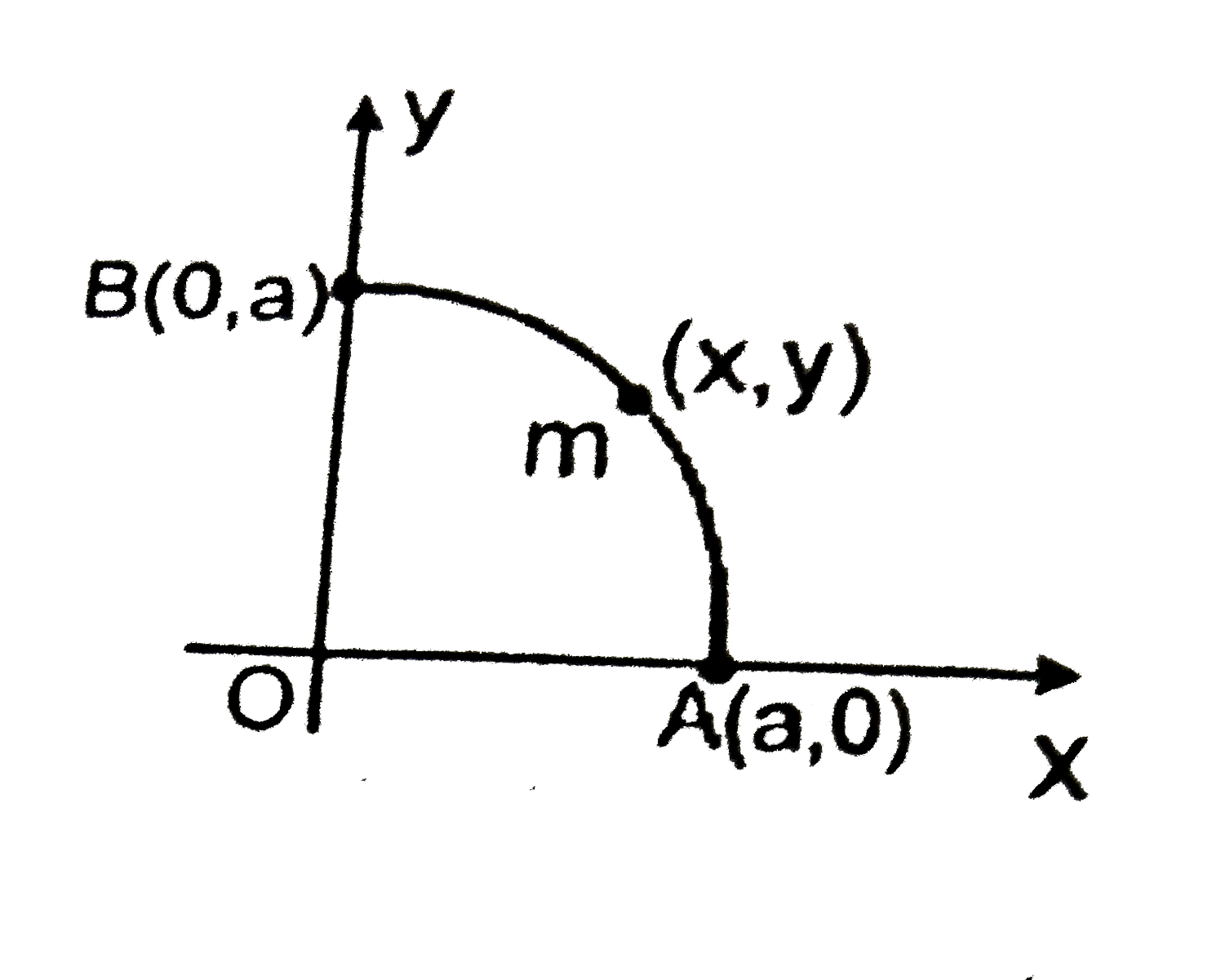
View SolutionA particle of mass 2kg moves under a force given by
→F=−(8N/m)(xˆi+yˆj)
where ˆi and ˆj are unit vectors in the x and y directions.
The particle is projected from the origin in xy plane with an initial velocity →v=(3m/s)ˆi+(4m/s)ˆj.
Select correct statement(s).
View SolutionWhen force →F1,→F2,→F3 are acting on a particle of mass m, the particle remains in equilibrium. If the force →F1 is now removed then the acceleration of the particle is :
View Solution
