A particle of mass $' m'$ moves along the quarter section of the circular path whose centre is at the origin . The radius of the circular path is $' a'$ . A force $\to F = y ˆ i - x ˆ j$ newton acts on the particle, where $x, y$ denote the coordinates of position of the particle. Calculate the work done by this force in taking, the particle from point, $A (a, 0)$ to point $B (0, a)$ along the circular path.

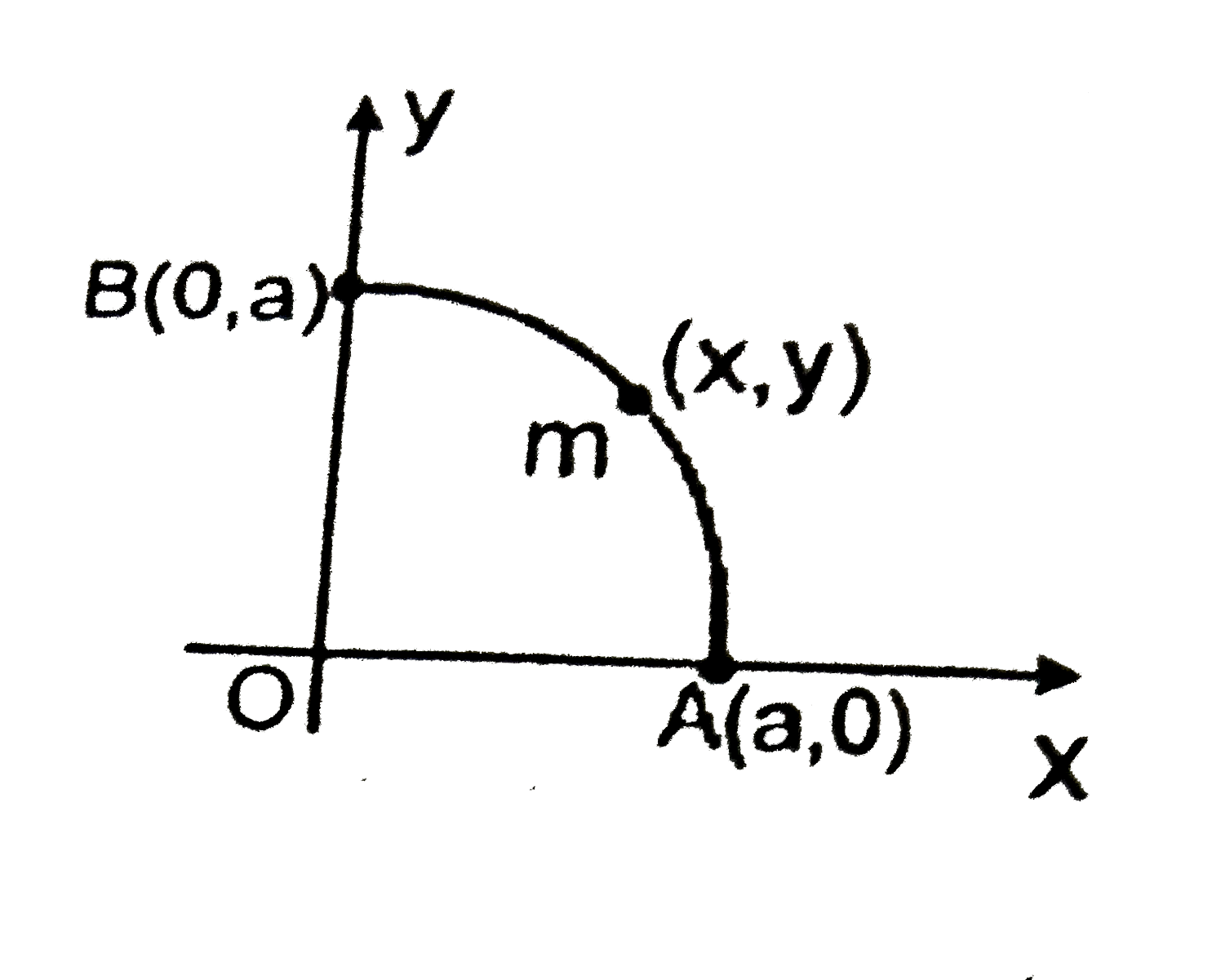
$π a^{2} J$

$\frac{π a^{2}}{2} J$

$- \frac{π a^{2}}{2} J$

Zero

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Updated on:21/07/2023

Answer

Step by step video & image solution for A particle of mass 'm' moves along the quarter section of the circular path whose centre is at the origin . The radius of the circular path is 'a'. A force vec(F)=yhat(i)-xhat(j) newton acts on the particle, where x,y denote the coordinates of position of the particle. Calculate the work done by this force in taking, the particle from point, A(a,0) to point B(0,a) along the circular path. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS QUESTION BANK

Knowledge Check

A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B

AAverage speed is v/2
BThe magnitude of average velocity is v/ $π$
CThe magnitude of average acceleration is $\frac{2 v^{2}}{π R}$
DAverage velocity is zero.

The correct Answer is:C

Similar Questions

Knowledge Check

A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B

Recommended Questions