A body is fired from point P and strikes at Q inside a smooth circular wall as shown in the figure. It rebounds to point S (diametrically opposite to P). The coefficient of restitution will be:
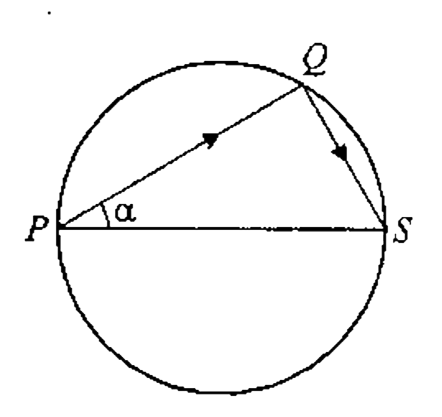
cotα
1
tanα
tan2α
The correct Answer is:D
Step by step video, text & image solution for A body is fired from point P and strikes at Q inside a smooth circular wall as shown in the figure. It rebounds to point S (diametrically opposite to P). The coefficient of restitution will be: by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION (II) : (SUBJECTIVE )
33 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION(II) : MCQ ( SINGLE CORRECT)
47 Videos
- KINEMATICSBOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - NUMERICAL BASED QUESTIONS
3 Videos
- HEAT AND TEMPERATUREBOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS
1 Videos
- LAWS OF MOTIONBOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III
2 Videos
Similar Questions
Knowledge Check
In the figure shown a particle P strikes the inclined smooth plane horizontally and rebounds vertically if the angle θ is 60∘ then the coefficient of restitution is:
 A1/3B1/√2C1/2D1
A1/3B1/√2C1/2D1A girl throws a ball with an initial velocity v at an angle 45∘. The ball strikes a smooth vertical wall at a horizontal distance d from the girl and after rebound returns to her hands. What is the coefficient of restitution between wall and ball ? (v2>dg)
Av2−gdgdBgdv2−gdCgdv2Dv2gd
A small ball is projected from point P towards a vertical wall as shown in Fig. It hits the wall when its velocity is horizontal. Ball reaches point P after one bounce on the floor. The coefficient of restitution assuming it to be same for two collisions is n/2. All surfaces are smooth. Find the value of n.

View SolutionA circular coil of radius R is moving in a magnetic filed B with a velocity v as shown in the figure.

Find the emf across the diametrically opposite points A and B.
View SolutionTwo charges are placed s shown in figure below. The potential at point P is
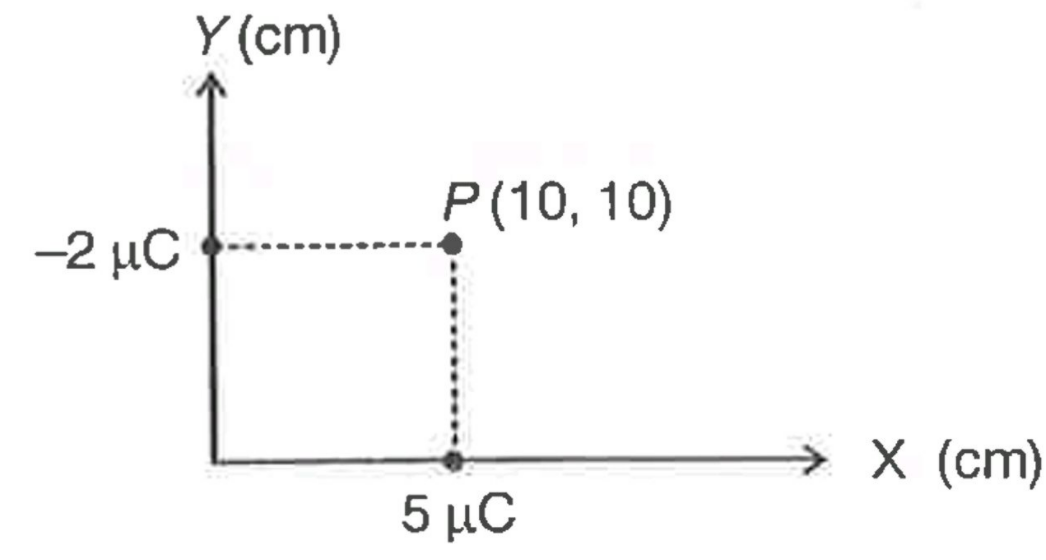
View SolutionThe point diametrically opposite to the point P(1,0) on the circle x2+y2+2x+4y−3=0 is :
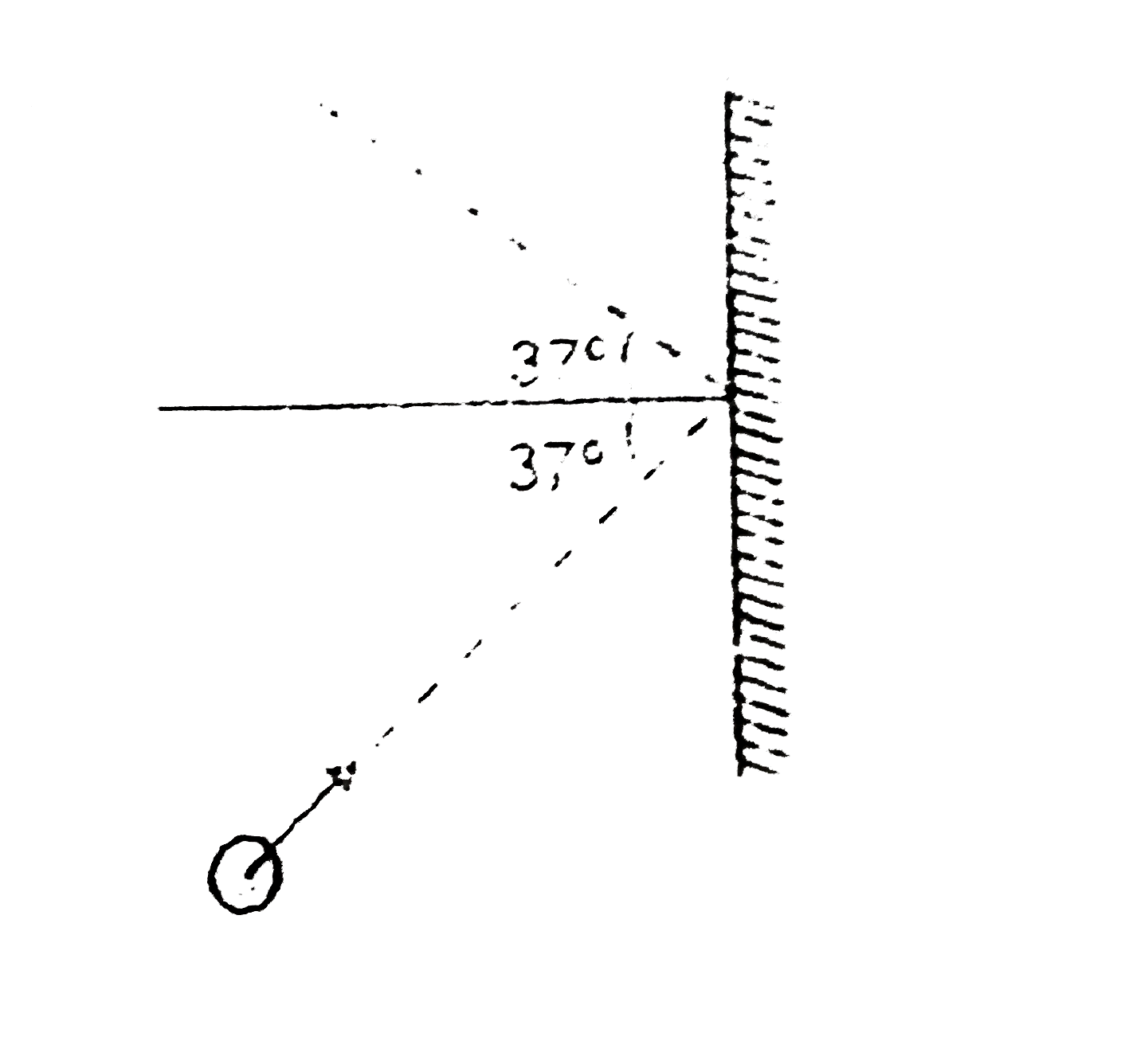
View SolutionA particle moving on a smooth horizontal surface strikes a stationary wall. The angle of strike is equal to the angle of rebound & is equal to 37∘ and the coefficient of restitution with wall is e=15. Find the friction coefficient between wall and the particle form X10 and fill value of X :
View SolutionThe point diametrically opposite to the point P(1, 0) on the circle x2+y2+2x+4y−3=0 is
View Solution

