Two particle are initially moving with angular momentum ${\to L}_{1}$ and ${\to L}_{2}$ in a region of space with no external torque. A constant external torque $\to τ$ then acts on one particle, but not on the other particle, for a time interval $Δ t$ . What is the chargne in the total angular momentum of the two particles ?

$- - \to Δ L = {\to L}_{1} - {\to L}_{2}$

$- - \to Δ L = \frac{1}{2} ({\to L}_{1} - {\to L}_{2})$

$- - \to Δ L = \to τ Δ t$

$- - \to Δ L$ is not applicable for this system

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

Answer

Step by step video, text & image solution for Two particle are initially moving with angular momentum vec(L)_(1) and vec(L)_(2) in a region of space with no external torque. A constant external torque vec( tau) then acts on one particle, but not on the other particle, for a time interval Delta t. What is the chargne in the total angular momentum of the two particles ? by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS KINEMATICS

Topper's Solved these Questions

Knowledge Check

Question 1 - Select One
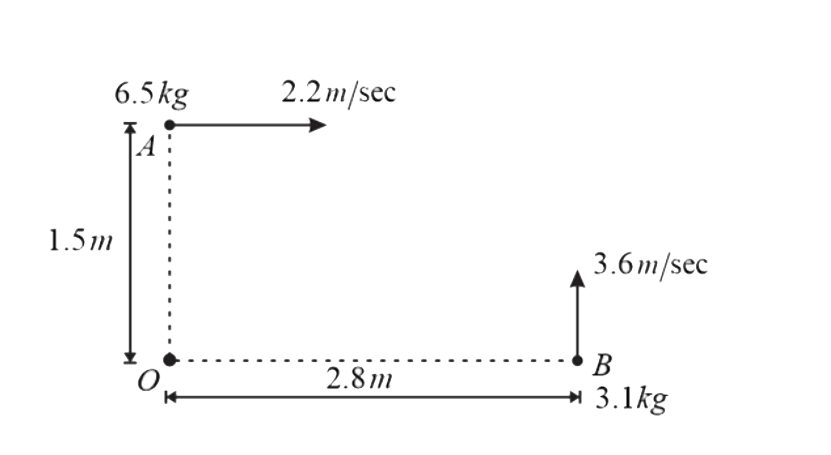
Two particle A and B are moving as shown in the figure

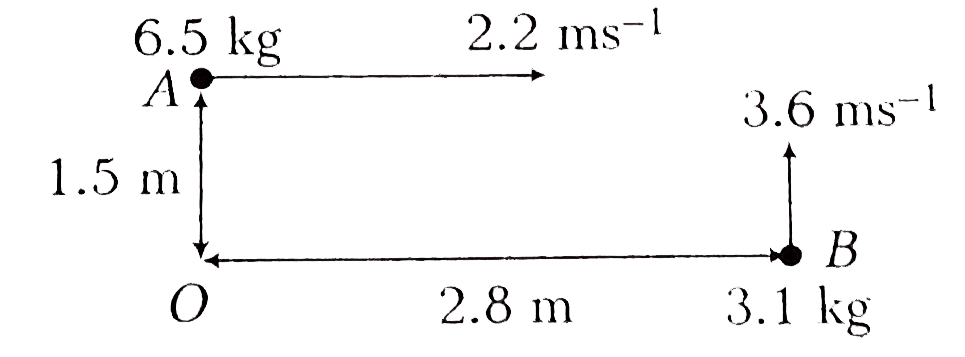
Their total angular momentum about the point O is
A $9.8 k g m^{2} s^{- 1}$
Bzero
C $52.7 k g m^{2} s^{- 1}$
D $37.9 k g m^{2} s^{- 1}$
Question 2 - Select One
Two particles A and B are moving as shown in the figure. Their total angular momentum about the point O is

A $9.8 k g m^{2} / s$
Bzero
C $52.7 k g m^{2} / s$
D $37.9 k g m^{2} / s$
Question 3 - Select One
Centripetal acceleration of a particle of mass m moving in a circle of radius r is $4 / r^{2}$ . What is the angular momentum of the particle ?
A4 m/r
B $4 m / \sqrt{r}$
C $2 m \sqrt{r}$
D2 m/r

FIITJEE-KINEMATICS-SECTION(II) : MCQ ( SINGLE CORRECT)

Home
Ask Doubt
Profile

The correct Answer is:C

Topper's Solved these Questions

Similar Questions

Knowledge Check

Two particle A and B are moving as shown in the figure Their total angular momentum about the point O is

Two particles A and B are moving as shown in the figure. Their total angular momentum about the point O is

Centripetal acceleration of a particle of mass m moving in a circle of radius r is 4/r2. What is the angular momentum of the particle ?

FIITJEE-KINEMATICS-SECTION(II) : MCQ ( SINGLE CORRECT)

Two particle A and B are moving as shown in the figure

Their total angular momentum about the point O is

Centripetal acceleration of a particle of mass m moving in a circle of radius r is $4 / r^{2}$ . What is the angular momentum of the particle ?