The adjacent figure shows a non-uniform metre stick AB having the linear mass density variation λ=λ0x , where λ0 is a constant and x is the distance from end A, placed on a smooth horizontal surface. In the first experiment, the rod is pivoted at A and force F is applied perpendicular to the rod at the other end B and in the second experiment, the rod is pivoted at B and the force is applied perpendicular to the rod at the end A. If in the first case angular acceleration is αA and in the second case it is αB then
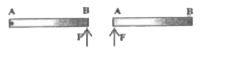
αA=αB
αA>αB
αA<αB
data insufficient to determine
The correct Answer is:C
Step by step video, text & image solution for The adjacent figure shows a non-uniform metre stick AB having the linear mass density variation lambda = lambda_(0) x , where lambda_(0) is a constant and x is the distance from end A, placed on a smooth horizontal surface. In the first experiment, the rod is pivoted at A and force F is applied perpendicular to the rod at the other end B and in the second experiment, the rod is pivoted at B and the force is applied perpendicular to the rod at the end A. If in the first case angular acceleration is alpha_(A) and in the second case it is alpha_(B) then by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - MCQ (MULTIPLE CORRECT)15videos
KINEMATICS
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - ASSERTION-REASON MCQ ( SINGLE CORRECT)8videos
KINEMATICS
- BOOK - FIITJEECHAPTER - KINEMATICSEXERCISE - SECTION (II) : (SUBJECTIVE )33videos
KINEMATICS
- BOOK - FIITJEECHAPTER - HEAT AND TEMPERATUREEXERCISE - NUMERICAL BASES QUESTIONS1videos
HEAT AND TEMPERATURE
- BOOK - FIITJEECHAPTER - LAWS OF MOTIONEXERCISE - COMPREHENSION-III2videos
LAWS OF MOTION
Similar Questions
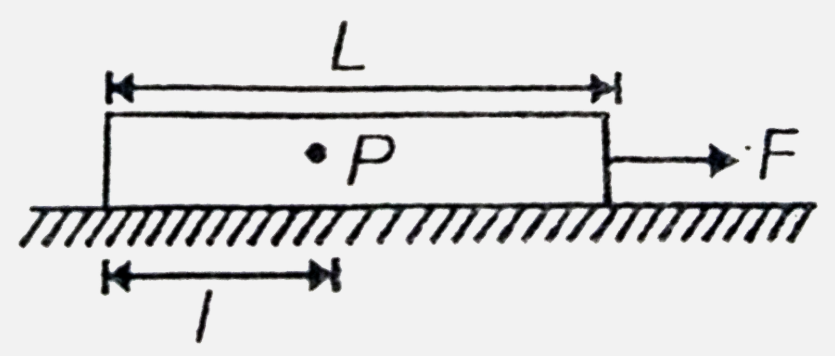
Figure shows a rope of variable mass whose linear mass density is given by , λ=Ax , where A is + ve constant and x is distance from left end . It b is placed on a smooth horizontal surface . A force F is acting on it as shown .
(i) Find total mass of the rope .
(ii) Find tension at point P.
 View Solution
View SolutionCalculate Centre of mass of a non-uniform rod with linear mass density γ

λ(mass/length)=kx2View Solution
Knowledge Check
- Question 1 - Select One
The mass per unit length of a non - uniform rod of length L is given μ=λx2 , where λ is a constant and x is distance from one end of the rod. The distance of the center of mas of rod from this end is
AL2BL4C3L4DL3 - Question 2 - Select One
A uniform rod of mass m, length l rests on a smooth horizontal surface. Rod is given a sharp horizontal impulse p perpendicular to the rod at a distance l/4 from the centre. The angular velocity of the rod will be
A3pmlBpmlCp2mlD2pml - Question 3 - Select One
The mass per unit length of a non-uniform rod of length L is given by μ=λ×2, where λ is a constant and x is distance from one end of the rod. The distance of the center of mass of rod from this end is :-
AL2BL4C3L4DL3
Find coordinates of mass center of a non-uniform rod of length L whose linear mass density lambda varies as lambda=a+bx, where x is the distance from the lighter end.
View SolutionThe centre of mass of a non uniform rod of length L whose mass per unit length λ=Kx2/L where K is a constant and x is the distance from one end is
(A) 3L4
(B) L8
(C) KL
(D) 3KLView SolutionA uniform rod AB of mass m and length l is at rest on a smooth horizontal surface. An impulse J is applied to the end B perpendicular to the rod in horizontal direction. Speed of the point A of the rod after giving impulse is:
View SolutionA uniform rod of mass m and length l is on the smooth horizontal surface. When a constant force F is applied at one end of the rod for a small time t as shown in the figure. Find the angular velocity of the rod about its centre of mass.
 View Solution
View SolutionA slender rod of mass M and length L rests on a horizontal frictionless surface. The rod is pivoted about one of ends. The impulse of the force exerted on the rod by the pivot when the rod is struck by a blow of impulse J perpendicular to the rod at other end is
View Solution

