A particle of mass m is thrown horizontally from point P , as shown in the figure, with speed 5m/s. It strikes an inclined plane perpendicularly as shown. The inclination of the plane is 30∘ with the horizontal. Then, the height h shown in the figure is ( Take g=10m/s2 ) .
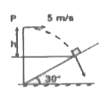
3.75m
5.0m
4.75m
0.417m
The correct Answer is:A
Topper's Solved these Questions
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:MCQ (MULTIPLE CORRECT)
Explore 15 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:ASSERTION-REASON MCQ ( SINGLE CORRECT)
Explore 8 Videos
- KINEMATICSBook:FIITJEEChapter:KINEMATICSExercise:SECTION (II) : (SUBJECTIVE )
Explore 33 Videos
- HEAT AND TEMPERATUREBook:FIITJEEChapter:HEAT AND TEMPERATUREExercise:NUMERICAL BASES QUESTIONS
Explore 1 Video
- LAWS OF MOTIONBook:FIITJEEChapter:LAWS OF MOTIONExercise:COMPREHENSION-III
Explore 2 Videos
Similar Questions
A particle is thrown horizontally from the top of an inclined plane , with a speed of 5m/s . If the inclination of the plane is 30∘ with the horizontal , how far from the point of projection will the particle strike the plane ?
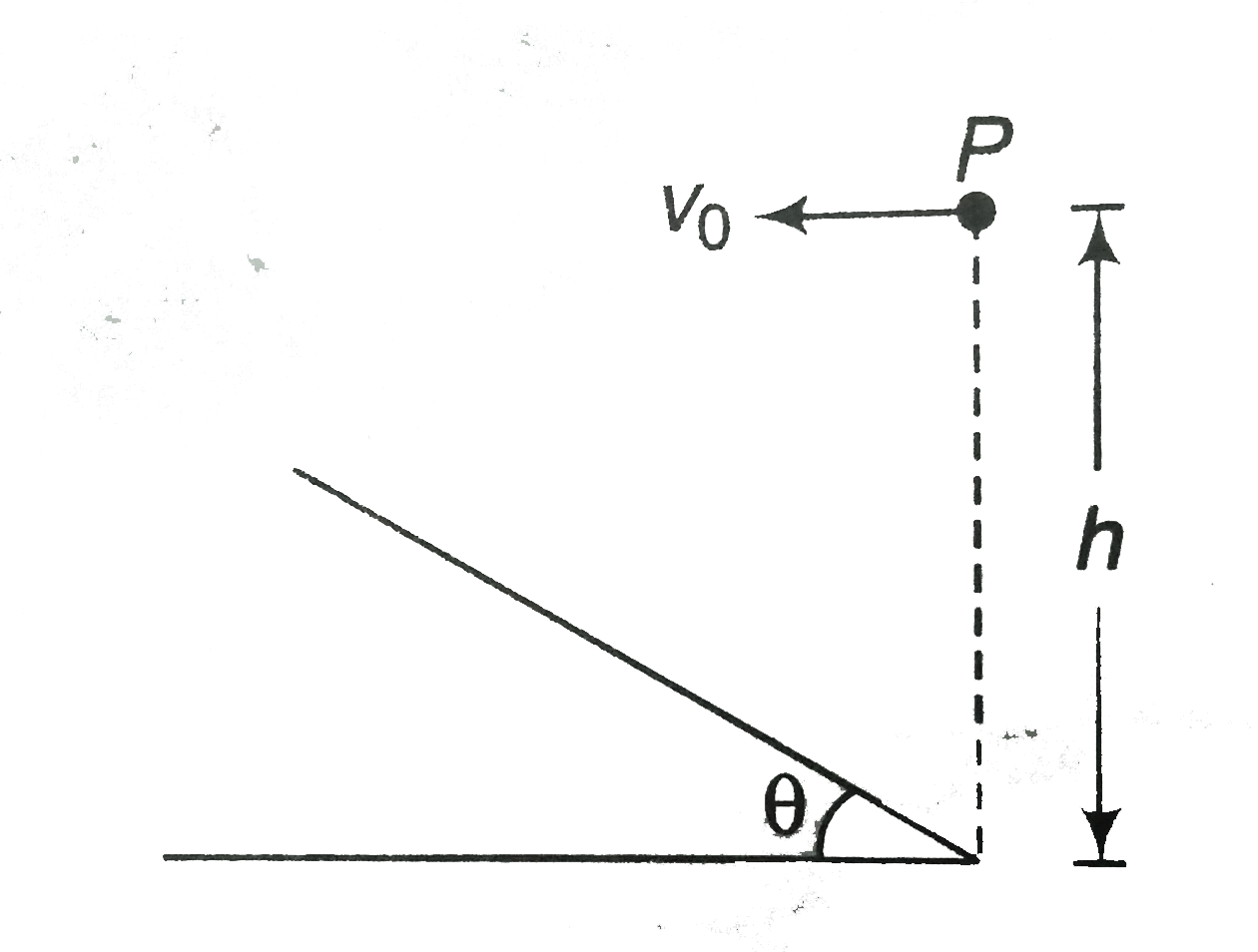
View SolutionDetermine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.
View Solution
Knowledge Check
A ball is thrown horizontally from a point O with speed 20 m/s as shown. Ball strikes the incline along normal after two seconds
The speed of ball just before striking the plane is:
 A20 m/sB20√2m/sC20√5m/sDnone
A20 m/sB20√2m/sC20√5m/sDnoneA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time
 Av0√3gB2v0√3gCv0gD2√3v0g
Av0√3gB2v0√3gCv0gD2√3v0gA partile is projected up an incline (inclination angle =30∘) with 15√3m/s at an angle of 30∘ with the incline (as shown in figure) (g=10m/s2)
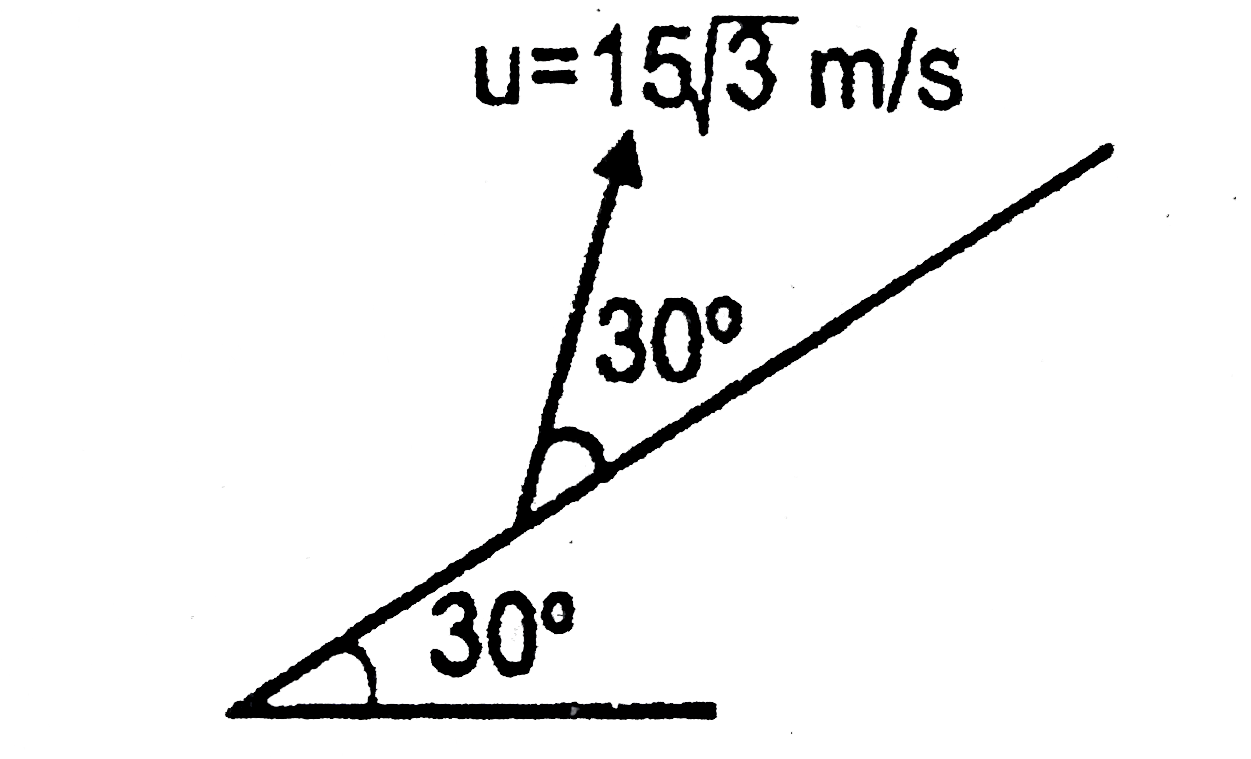 A1.5 sec later, angle between acceleration & velocity is 120∘B1.5 sec later, angle between acceleration & velocity is 60∘.CRange on the incline is 45mDTime of flight on the incline is 3 sec.
A1.5 sec later, angle between acceleration & velocity is 120∘B1.5 sec later, angle between acceleration & velocity is 60∘.CRange on the incline is 45mDTime of flight on the incline is 3 sec.
Determine the horizontal velocity v0 with which a stone must be projected horizontally from a point P, so that it may hit the inclined plane perpendicularly. The inclination of the plane with the horizontal is θ and point P is at a height h above the foot of the incline, as shown in the figure.

View SolutionA particle is projected with velocity "u" in horizontal direction as shown in the figure. Find u if particle collides perpendicularly with inclined plane. h
View SolutionA ball is thrown horizontally from a point O with speed 20 m/s as shown. Ball strikes the incline along normal after two seconds
The speed of ball just before striking the plane is:

View SolutionA ball is projected horizontally from an inclined plane with a velocity V, as shown in the figure. It will strike the plane after a time

View SolutionA particle is projected with velocity "u" in horizontal direction as shown in the figure. Find u if particle collides perpendicularly with inclined plane. u
View Solution
