Let f(x+y2)=f(x)+f(y)2 for all real x and y. If f'(0) exists and equals-1 and f(0)=1, find f(2)
Suppose A(x,f(x))andB(y,f(y)) be any two points on the curve y=f(x).
If M is the mid-point of AB, then the coordinates of M are (x+y2,f(x)+f(y)2).
Now the foot of the perpendicular from the M on the x-axis is L. ML meets the curve y=f(x) at P.
According to the graph, the coordinates of P are (x+y2,f(x+y2))andPL>ML.
⇒ f(x+y2)>f(x)+f(y)2
But given f(x+y2)=f(x)+f(y)2, which is possible when P→M.
That is, P lies on AB. Hence y=f(x) must be a linear function.
Let f(x)=ax+b ⇒f(0)=0+b=1 (given )
and f'(x)=a ⇒f'(0)=a=−1 (given )
∴ f(x)=−x+1
∴ f(2)=−2+1=−1
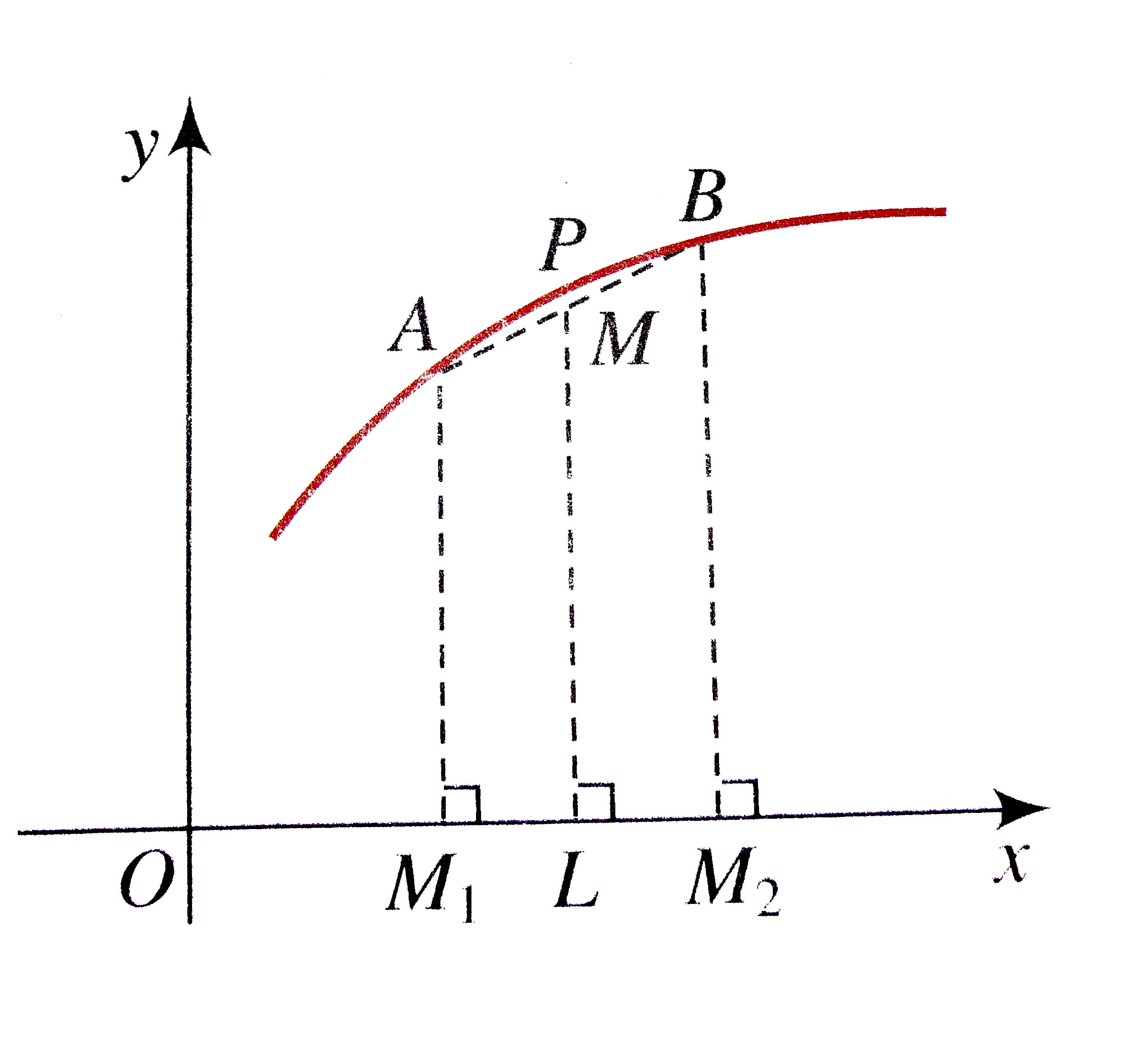
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Let f(x+y)=f(x)f(y) for all x and y. If f(5)=2 and f'(0)=3 then f'(5) is equal to
A5B8C0Dnone of these - Question 2 - Select One
Let f(x+y)=f(x)+f(y)−2xy−1 for all x and y. If f'(0) exists and f'(0)=−sinα, then f{f'(0)} is
A-1B0C1D2 - Question 3 - Select One
If f(x+y)=f(x)f(y) for all real x and y, f(6)=3 and f'(0)=10, then f'(6) is equal to
A30B13C10D0
Let f(x+y)−f(x)2=f(y)−a2+xy for all real xandy. If f(x) is differentiable and f′(0) exists for all real permissible value of a and is equal to √5a−1−a2. Then f(x) is positive for all real x f(x) is negative for all real x f(x)=0 has real roots Nothing can be said about the sign of f(x)
View SolutionLet f(x+y)=f(x)+f(y) for all real x,yandf'(0) exists. Prove that f'(x)=f'(0) for all x∈Rand2f(x)=xf(2).
View Solutionif f(x+y)=f(x)+f(y)+c, for all realx and y and f(x) is continuous at x=0 andf'(0)=−1 then f(x) equals to
View SolutionLetf(x+y)=f(x)f(y)for all x,y, wheref(0)≠0. If f'(0)=2, then f(x) is equal to
View SolutionIf f(x+y)=f(x)f(y) for all real x and y, f(6)=3 and f'(0)=10, then f'(6) is
View Solution

