If $x < 2$ , then find the values of $x^{2}$ graphically.

Video Solution

Text Solution

Verified by Experts

In such cases, generally students square both sides and get the answer $x^{2} < 4$ , which is wrong.
In such cases, we can take help of the graph of $y = x^{2}$ .

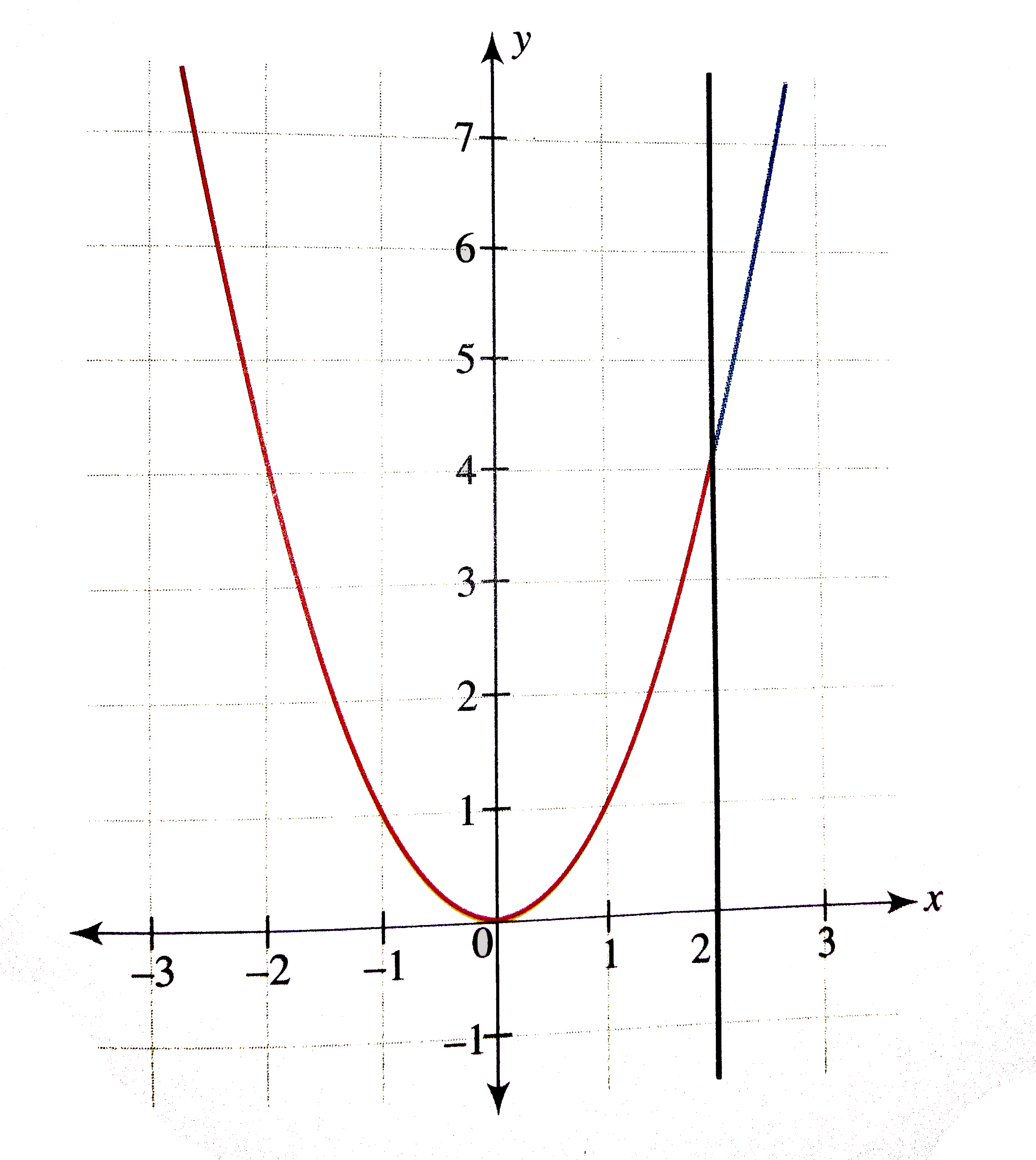
From the graph when $x = 2, x^{2} = 4$ .
For $0 > x > 2$ , the values of $x^{2}$ reduce form 4 to 0 and for $x > 0$ , the value of $x^{2}$ increase from 0 to $\infty$ (infinity).
Thus, we must consider the portion of the graph which is for $x > 2$ , in which $x^{2} \leq 0 or x^{2} \in [0, \infty)$ .

Updated on:21/07/2023