Question

Let $f\left(x\right)=2x(2-x),0\le x\le 2$. Then find the number of solutions of $f\left(f\left(f\left(x\right)\right)\right)=\frac{x}{2}$.

Explanation

We have `f(x)= 2x(2-x), 0 le x le 2`
The graph of `y= f(x)` is parabola, which is concave downwards as shown in the following figure.

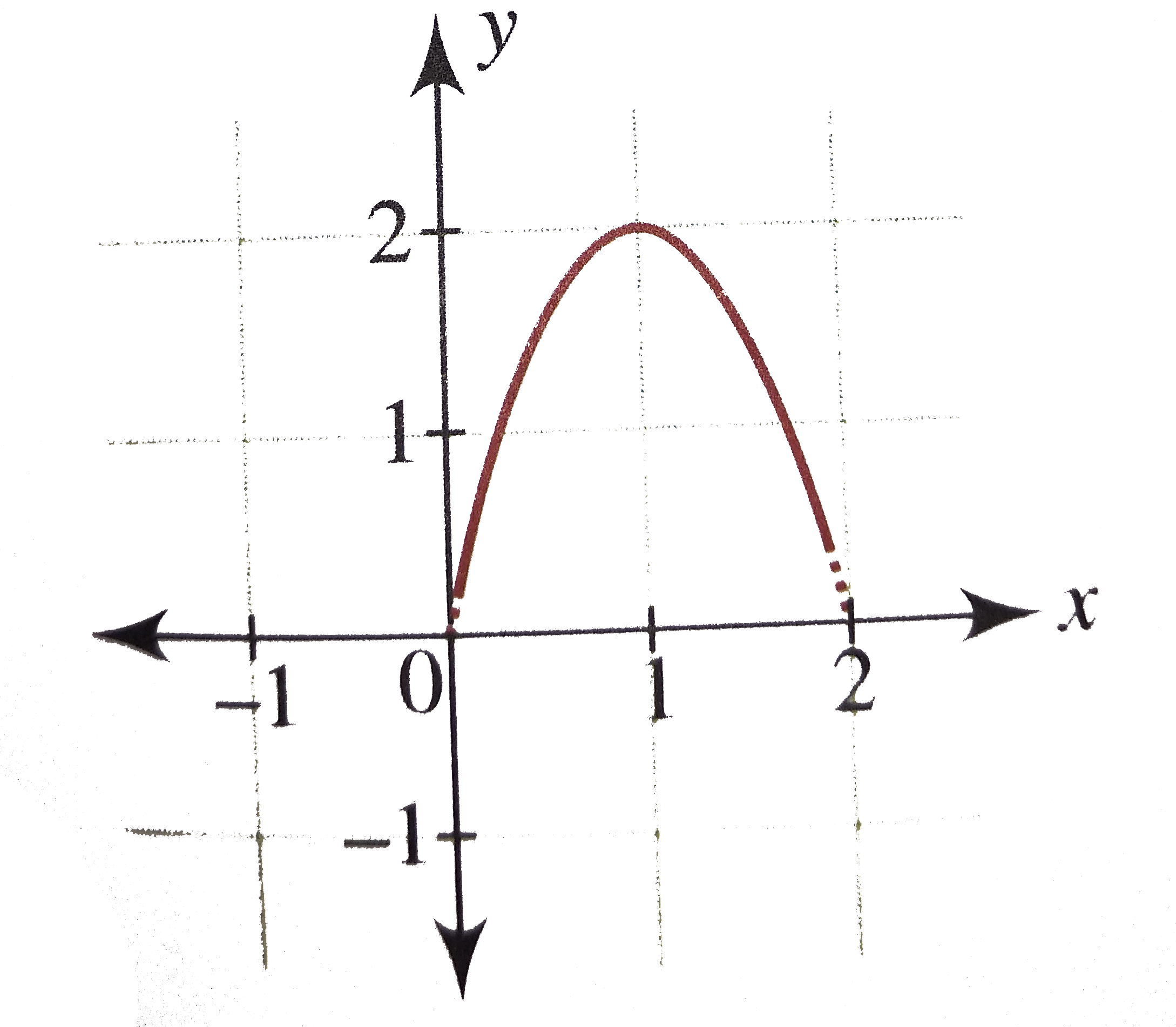
Range of `y= f(x)` is [ 0, 2 ].
Now `f(f(x))= 2f(x)(2-f(x))`, which is a fourth degree polynomial function.
`" "f(f(x))=0 theref0re f(x)=0 or f(x)=2`
`therefore" "x=0, 2 or 2x(2-x)=2`
`therefore" "x=0, 1, 1, 2`
Thus, `f(f(x))=0` has four roots in which one root is repeated.
Also the range of `y= f(f(x))` is [0, 2] as `f(x) in ` [0, 2] for `x in` [0, 2].
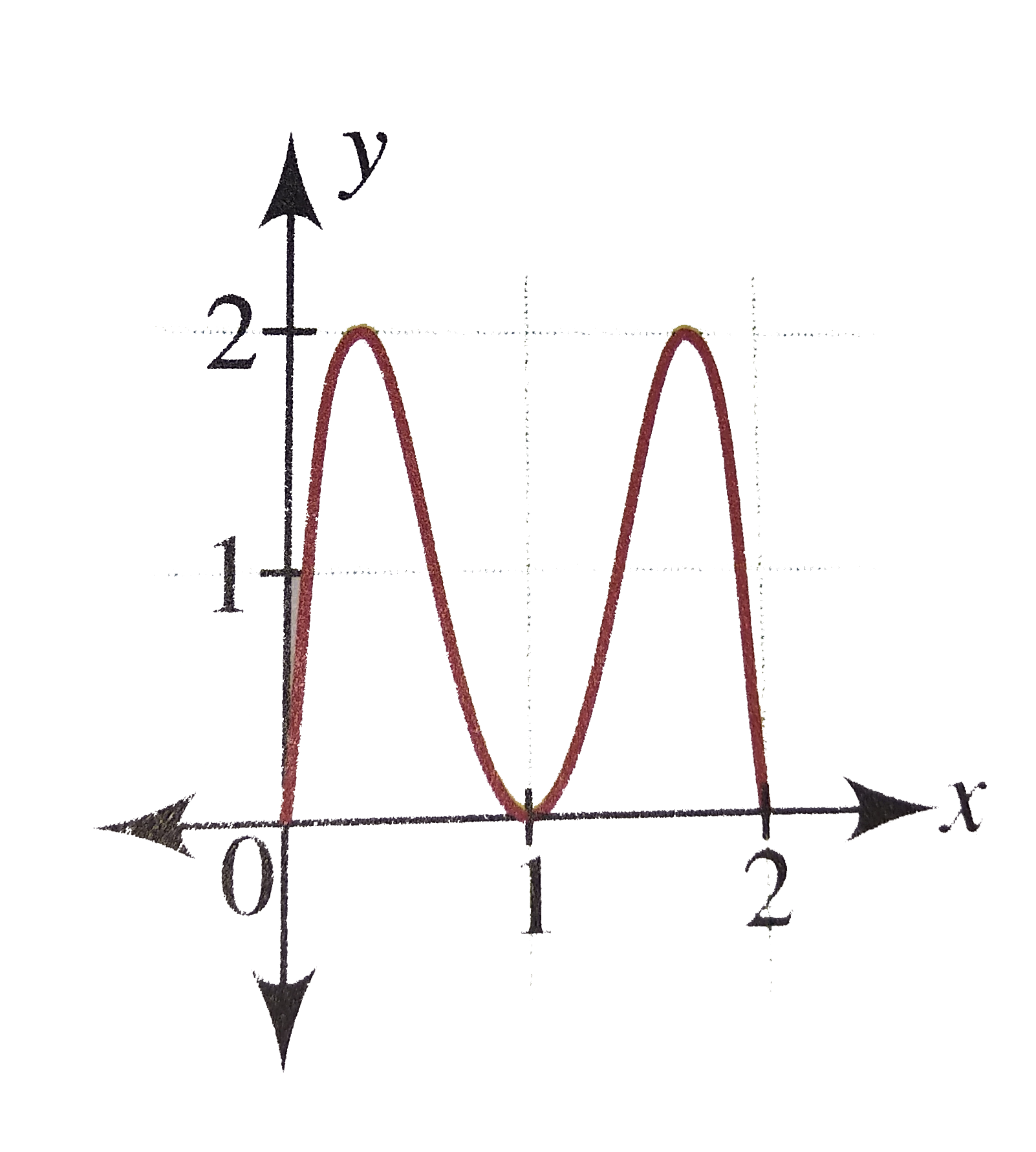
So the graph of `y=f(f(x))` is

With similar arguments, the graph of `y= f(f(f(x)))` is as follows :

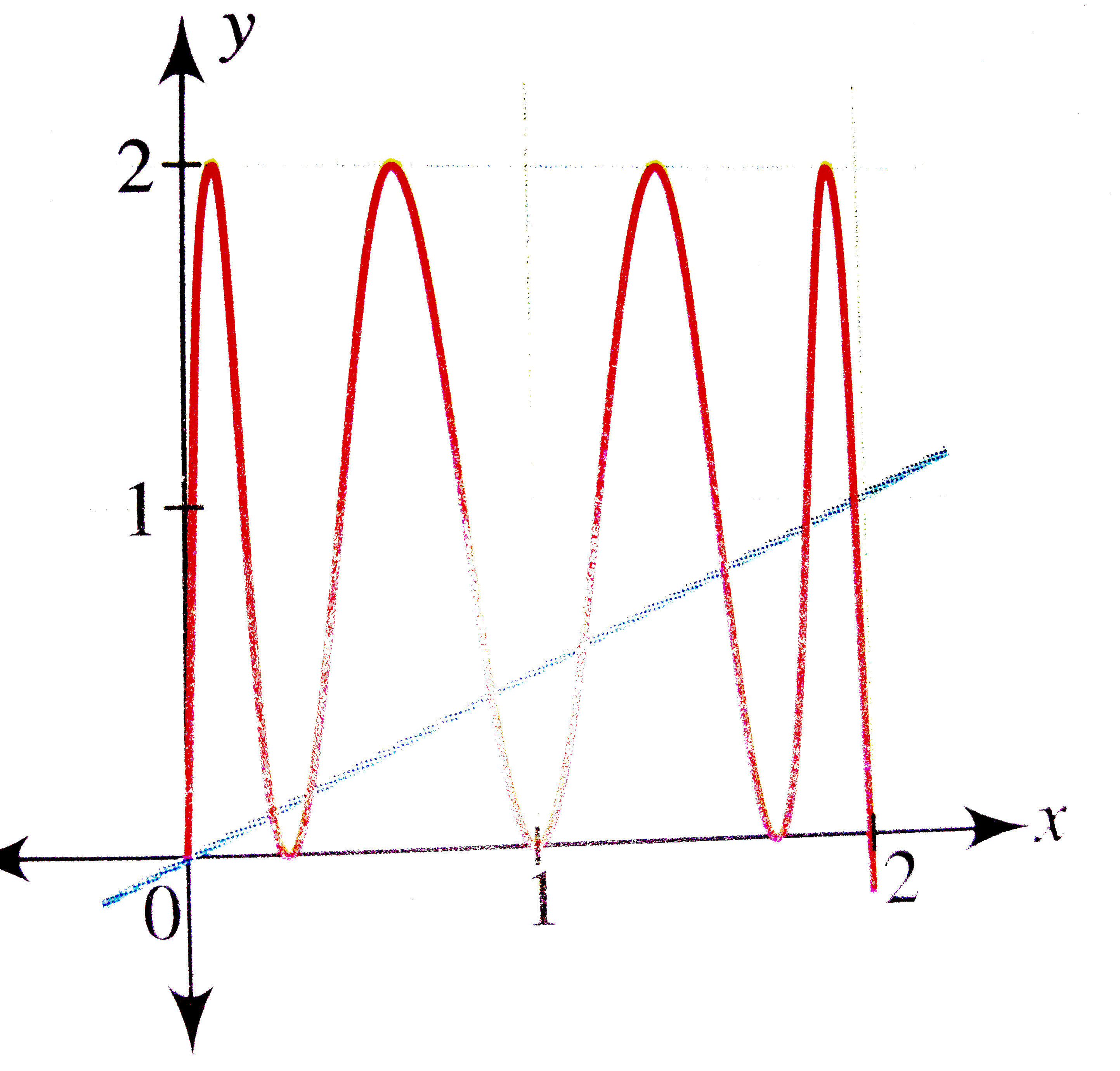
Clearly, the line `y=x//2` meets the graph of `y= f(f(x))` in eight points, hence '8' roots.