Question

If $b>a$, then the equation $(x-a)(x-b)-1=0$ has
(a) Both roots in $(a,b)$ (b) Both roots in $(-\infty ,a)$
(c) Both roots in $(b,+\infty )$ (d) One root in $(-\infty ,a)$ and the other in $(b,+\infty )$

Explanation

Given equation is `(x-a)(x-b)-1=0`
Let `" "f(x)= (x-a)(x-b)-1`
`" "f(a)=-1`
and `" "f(b)=-1`
Graph of `f(x)` is concave upwards, hence `a and b` lie between the roots.

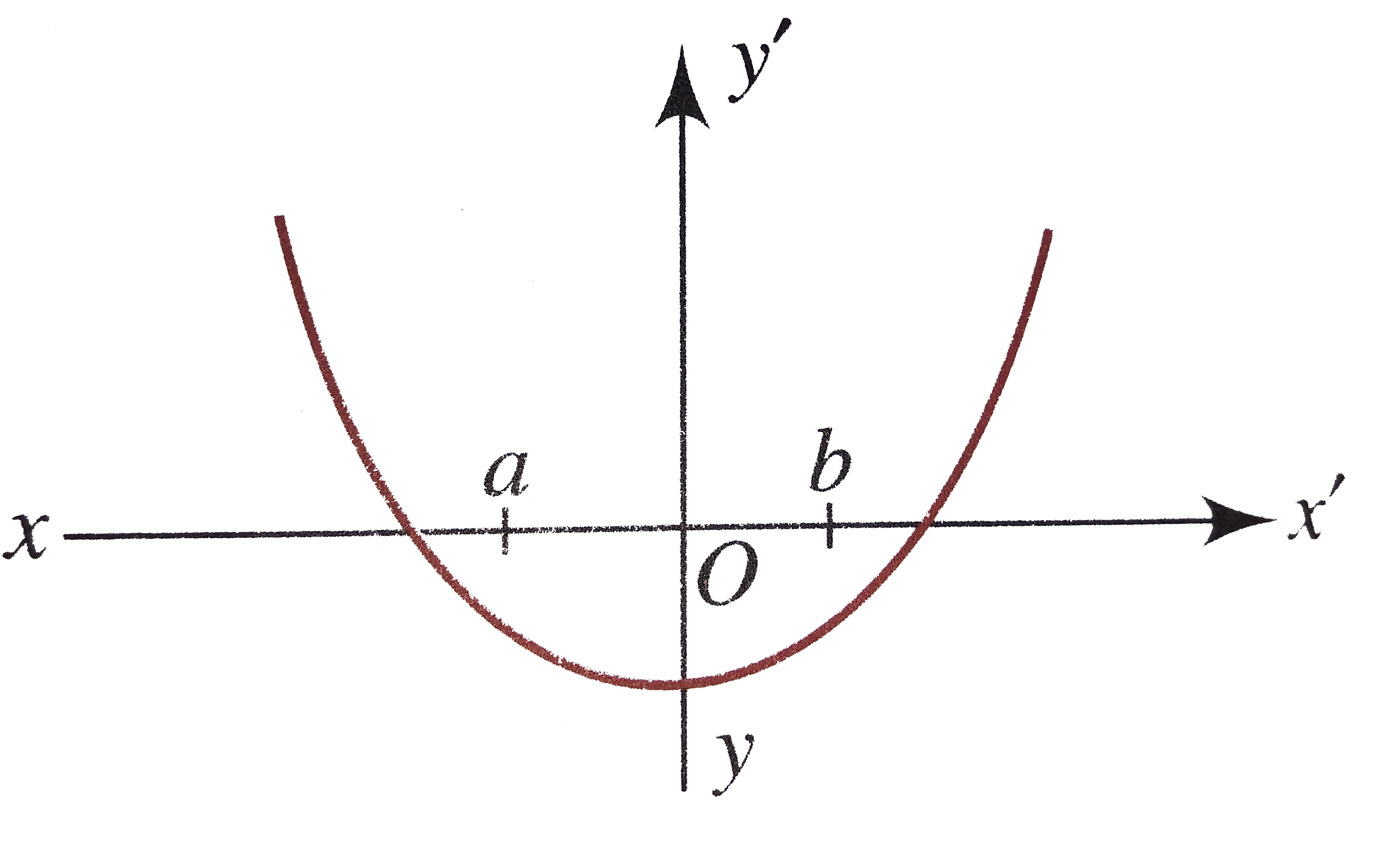
Also `b gt a`, then one root is in `(-oo, a)` and the other is in `(b, +oo)`.