If 2≤|x|≤5, then find the values of x from the graph of y=|x|.
Draw the graph of y=|x| and lines y=2andy=5.
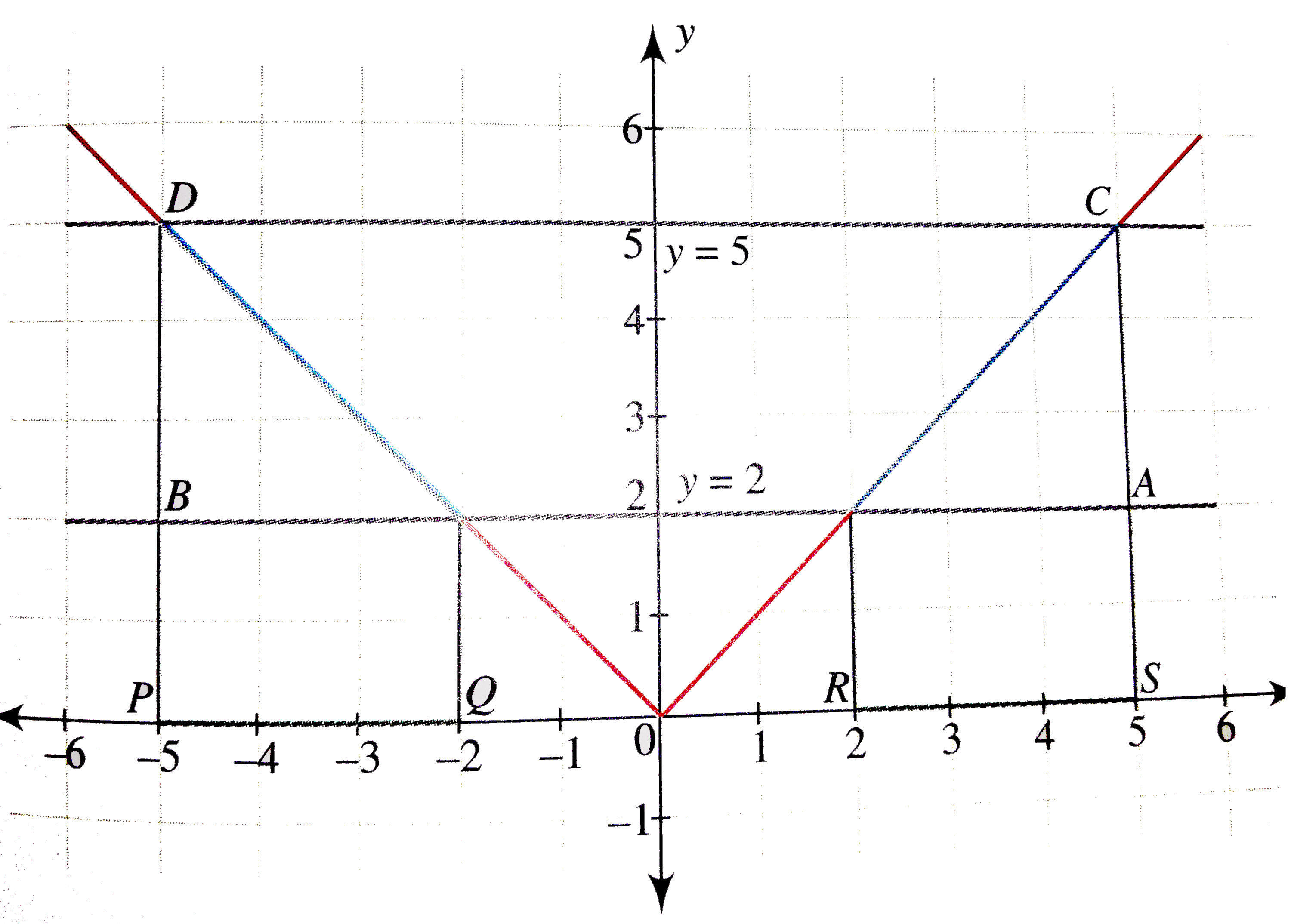
Line y=2 meets y=|x| at A(2,2)andB(−2,−2). From these points, drop perpendicular to the x-axis.
Line y=5 meets y=|x| at C(5,5)andD(−5,−56). From these points, drop perpendiculars to the x-axis.
From the graph, required values of x are between P and Q and between R and S.
Therefore,
x∈[−5,−2]∪[2,5]
Topper's Solved these Questions
- BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise34videos
GRAPHS OF ELEMENTARY FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise13videos
GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONS
- BOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise22videos
GRAPHS OF TRIGONOMETRIC FUNCTIONS
Similar Questions
Draw the graph of y≤x+2.
View SolutionS={3x2≤4y≤6x+2y} find the area
View SolutionFor 2<x<4 find the values of |x|.
(ii) For −3≤x≤−1, find the values of |x|.
(iii) For −3≤x<1, find the values of |x|
(iv) For −5<x<7 find the values of |x-2|
(v) For 1≤x≤5 find fthe values of |2x -7|View SolutionIf x+y≤5, then either x≤5ory≤5 or both (True/False)
View SolutionFind the area of the region {(x,y):x2≤y≤|x|}.
View SolutionIf 0≤x≤4,0≤y≤8,x+y≤8, then maximum of z=5x+3y is
View SolutionIf 0≤x≤3π,0≤y≤3πandcosx⋅siny=1, then find the possible number of values of the orederd pair (x,y) .
View SolutionFind the area of the region {(x,y):x2≤y≤x}
View SolutionFind the area of the region [ (x,y):x2≤y≤x)
View SolutionIf R1={(x,y)∣y=2x+7, where x∈R and −5≤x≤5} is a relation. Then find the domain and Range of R1.
View Solution

