Draw the graph of the function $f (x) = ∣ ∣ ∣ (x + \frac{1}{2}) [x] ∣ ∣ ∣, - 2 \leq x \leq 2$ , where $[\cdot]$ denotes the greatest integer function. Find the points of discontinuity and non-differentiability.

Text Solution

Verified by Experts

Here, $f (x) = ∣ ∣ ∣ (x + \frac{1}{2}) [x] ∣ ∣ ∣, - 2 \leq x \leq 2$
$\Rightarrow f (x) = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} ∣ ∣ (x + \frac{1}{2}) (- 2) ∣ ∣, & - 2 \leq x < - 1 ∣ ∣ (x + \frac{1}{2}) (- 1) ∣ ∣, & - 1 \leq x < 0 ∣ ∣ (x + \frac{1}{2}) (0) ∣ ∣, & 0 \leq x < 1 ∣ ∣ (x + \frac{1}{2}) (1) ∣ ∣, & 1 \leq x < 2 ∣ ∣ \frac{3}{2} \cdot 2 ∣ ∣, & x = 2 \end{matrix}$
$\Rightarrow = ⎧ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎨ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎩ \begin{matrix} - (2 x + 1), & - 2 \leq x < - 1 - (x + 1 / 2), & - 1 \leq x < - 1 / 2 (x + 1 / 2), & - \frac{1}{2} \leq x < 0 0, & 0 \leq x < 1 x + \frac{1}{2}, & 1 \leq x < 2 3, & x = 2 \end{matrix}$
The graph of the function is as shown in the following figure.

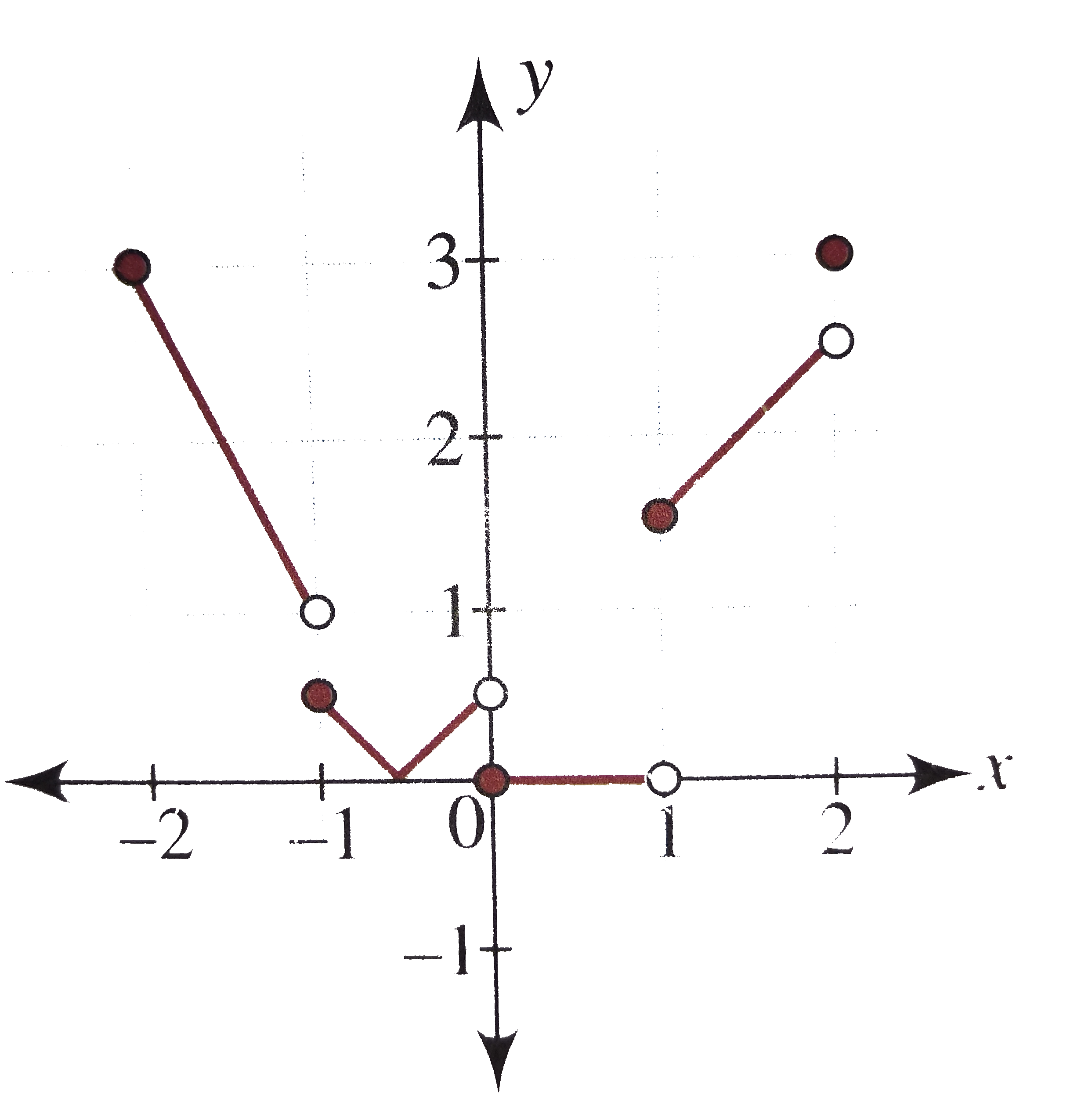
From the figure, $f (x)$ is not continuous as $x = {- 1, 0, 1, 2}$ as at these points, the graph is broken and $f (x)$ is not differentiable.
At $x = {- 1, \frac{- 1}{2}, 0, 1, 2}$ as at ${- 1, 0, 1, 2}$ , the graph is broken and $x = - 1 / 2$ , there is a sharp edge.

Updated on:21/07/2023

|

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Let $f (x) = \frac{x^{2} + 2}{[x]}, 1 \leq x \leq 3$ , where [.] is the greatest integer function. Then the least value of f(x) is
A2
B3
C $3 / 2$
D1

CENGAGE-GRAPHS OF ELEMENTARY FUNCTIONS -Exercise

Home
Ask Doubt
Profile