Doubtnut Promotions Sticky

Draw the graph of f(x)=[logex],e−2<x<10, where [⋅] represents the greatest integer function.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We have f(x)=[logex],e−2<x<10 ltBrgt logex is an incresing function in its entire domain.
So [logex] is discontinuous when logex is an integer.
Now e−2<x<10
∴ −2<logex<10
So [logex] is discontinuous when logex=−1,0,1,2.
∴ x=e−1,1,e,e2
∴ f(x)=[logex]=⎧⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎨⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎩−2,x∈[e−2,e−1)orlogex∈[−2,−1)−1,x∈[e−1,1)orlogex∈[−1,0)0,x∈[1,e)orlogex∈[0,1)1,x∈[e,e2)orlogex∈[1,2)2,x∈[e2,10)orlogex∈[2,loge10)
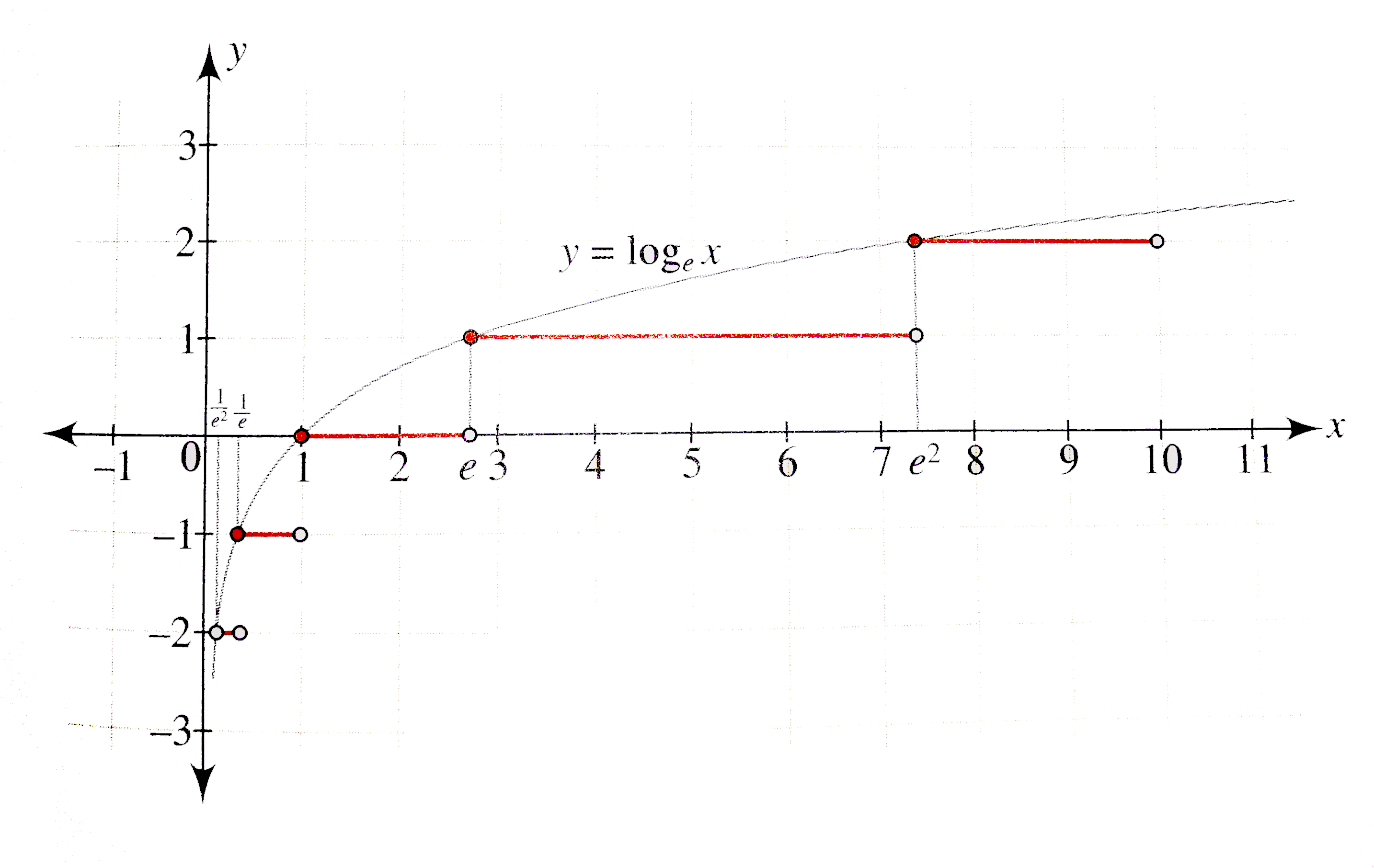
ocr_image

|
Updated on:21/07/2023
Class 12MATHSFUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One or More

    If f(x)=x(e|x|+[x]−2|x|+[x]) then (where [.] represent the greatest integer function)

    Alimx→0+f(x)=−1
    Blimx→0−f(x)=0
    Climx→0f(0)=−1
    Dlimx→0f(x)=0