Solve $x^{2} - 4 - [x] = 0$ (where $[]$ denotes the greatest integer function).

Video Solution

Text Solution

Verified by Experts

The best method to solve such an equation is graphical one.
Give equation is $x^{2} - 4 = [x]$ .
Then the solutions to the question are values of x where the graphs of $y = x^{2} - 4 and y = [x]$ interesect.

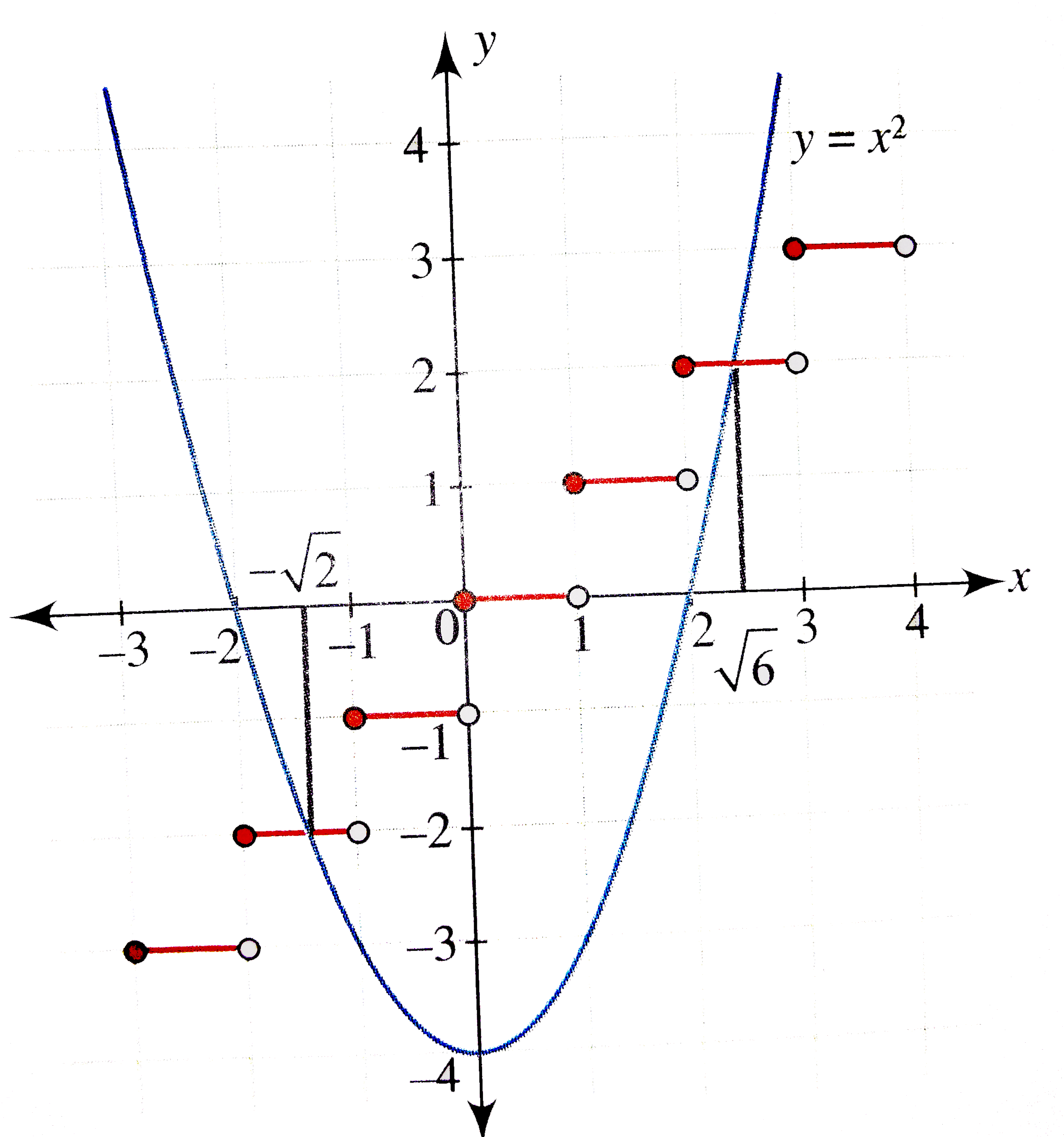
From the figure, it is seen that the graphs intersect when
$x^{2} - 4 = 2 and x^{2} - 4 = 2$ .
$\Rightarrow x^{2} = 6 or x^{2} k = 2$
$\Rightarrow x = x = \sqrt{6} or - \sqrt{2}$

|

Updated on:21/07/2023

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
If $f (x) = [x^{- 2} [x^{2}]]$ , (where $[\cdot]$ denotes the greatest integer function) $x \neq 0$ , then incorrect statement
Af(x) is continuous everywhere
Bf(x) is discontinuous at $x = \sqrt{2}$
Cf(x) is non-differentiable at x = 1
Df(x) is discontinuous at infinitely many points

CENGAGE-GRAPHS OF ELEMENTARY FUNCTIONS -Exercise

Home
Ask Doubt
Profile