Sketch the region of relation , where denots the greatest integer function.
Text Solution
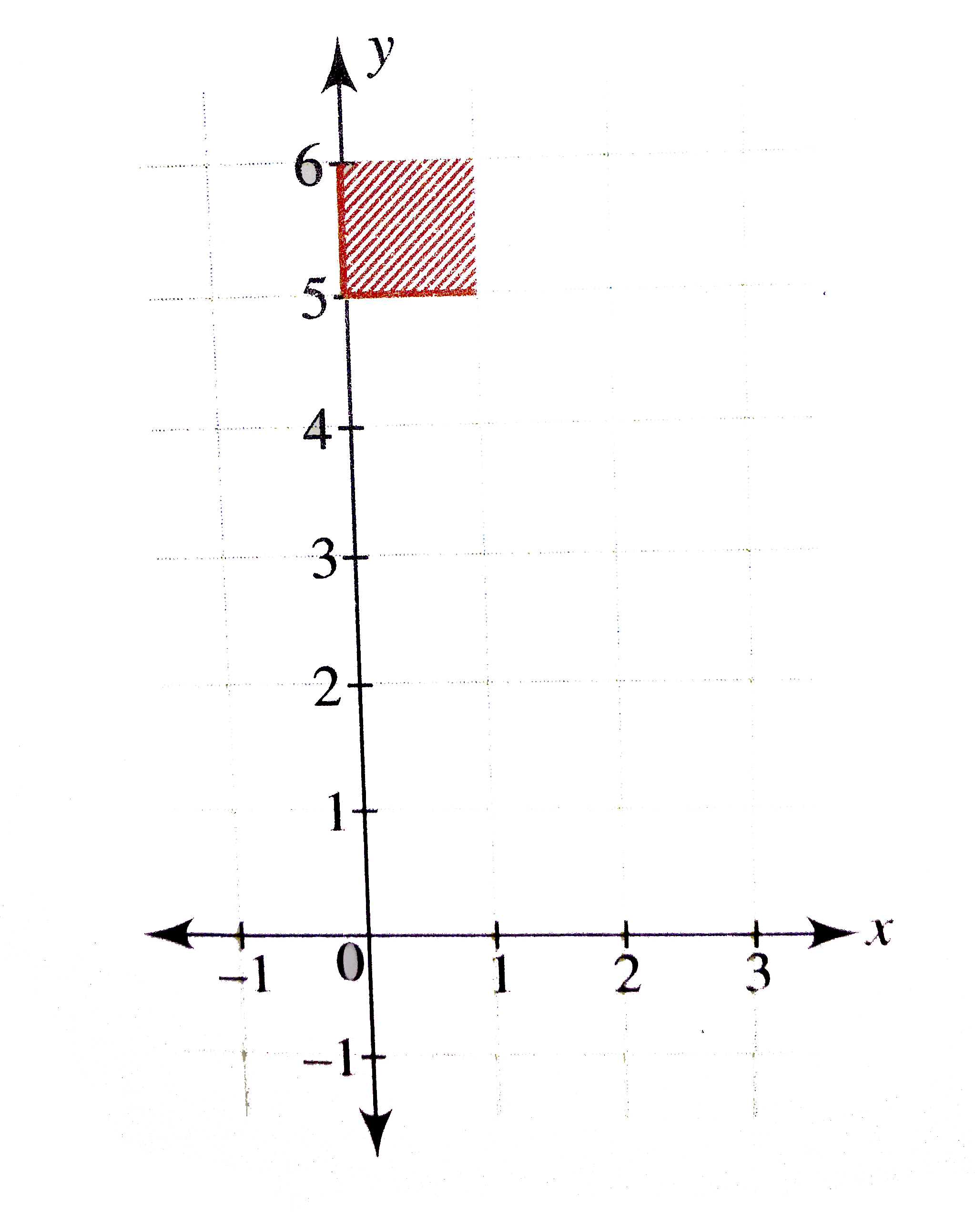
For
Thus, the points lie in the region stisfying as shown in the following figure.
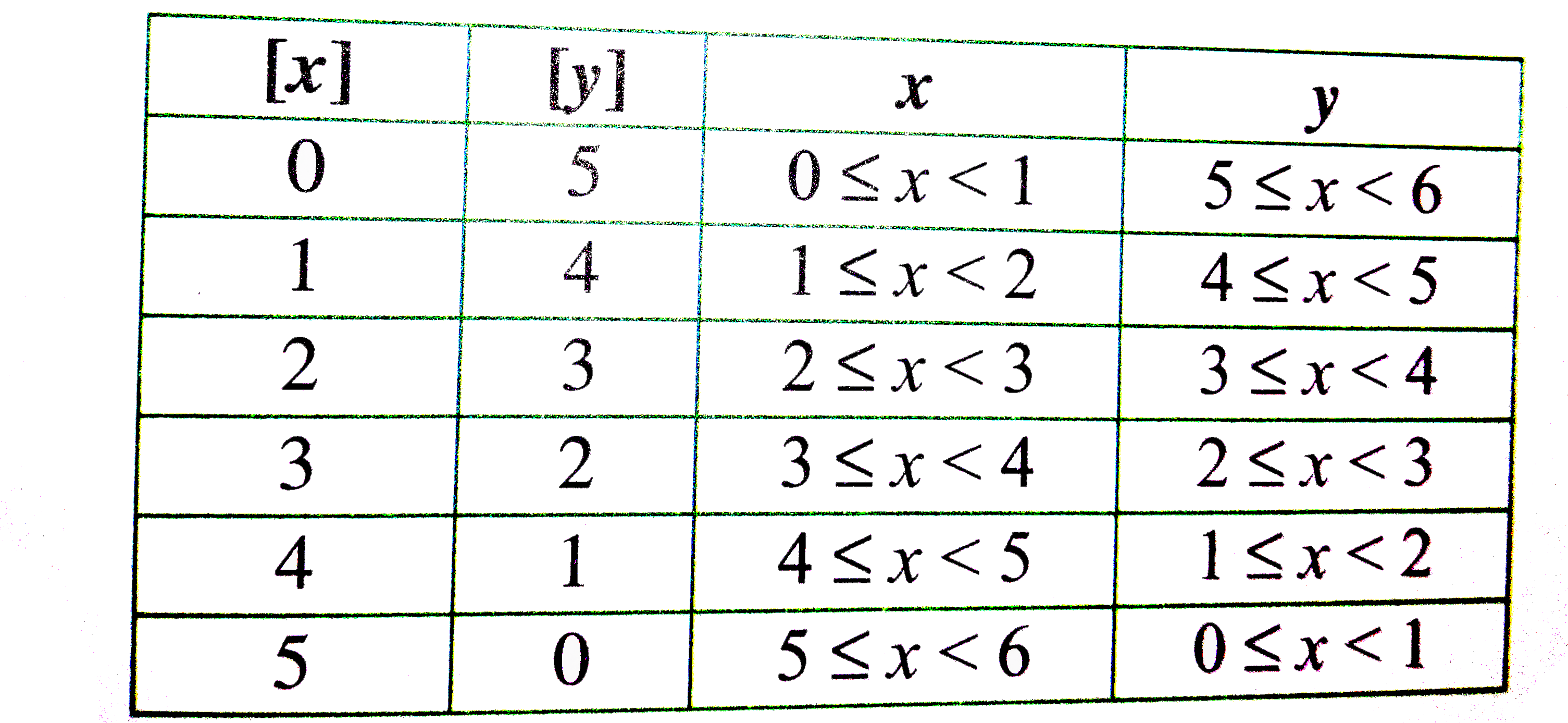
Thus, we have the following values of x and the corresponding values of y.
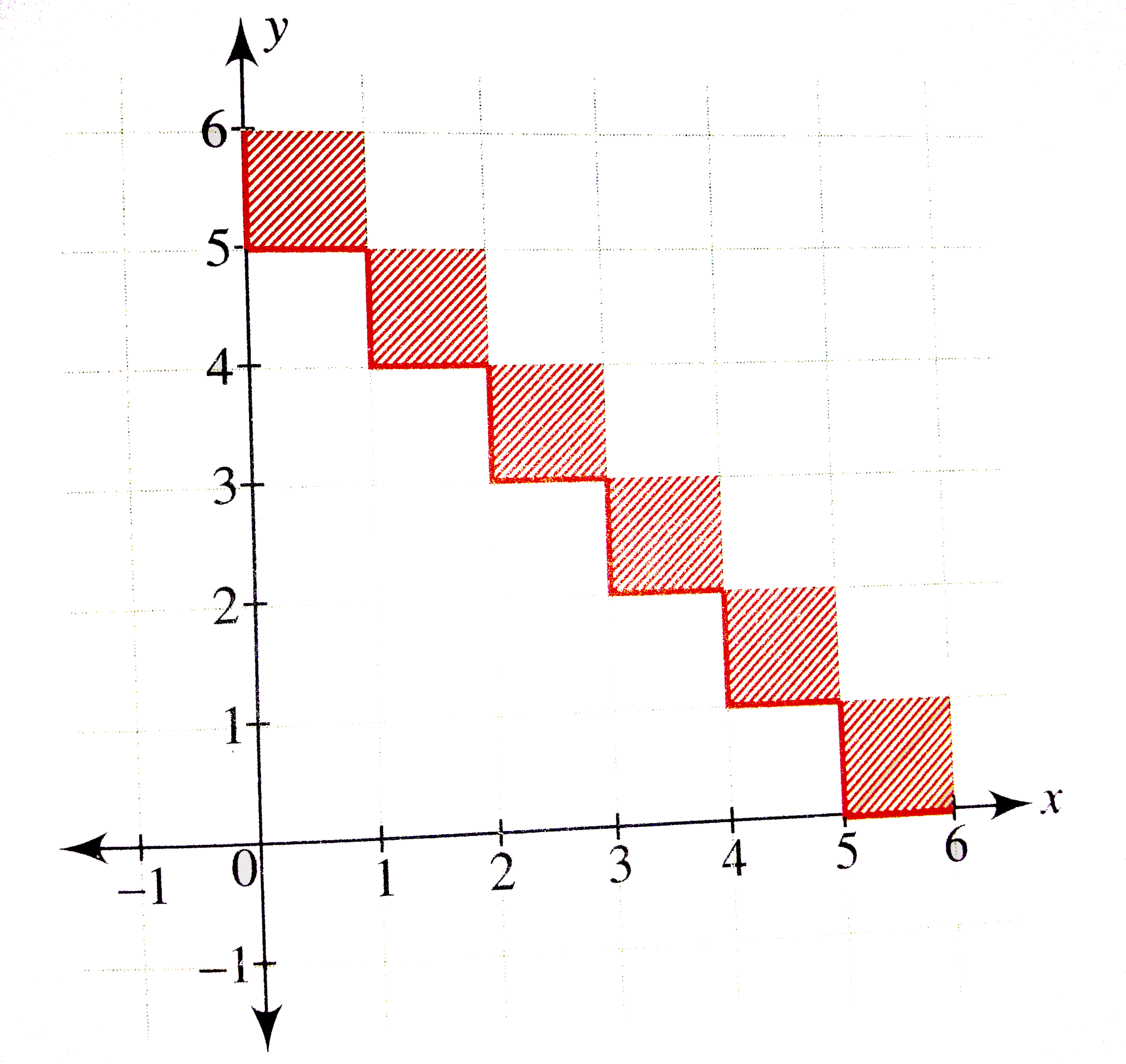
The region satisfying the above conditions is as shown in the following figure.
|
Topper's Solved these Questions
- GRAPHS OF ELEMENTARY FUNCTIONS Book:CENGAGEChapter:GRAPHS OF ELEMENTARY FUNCTIONS Exercise:Exercise
Explore 34 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBook:CENGAGEChapter:GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSExercise:Exercise
Explore 13 Videos
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBook:CENGAGEChapter:GRAPHS OF TRIGONOMETRIC FUNCTIONSExercise:Exercise
Explore 22 Videos
Similar Questions
Knowledge Check
∫50[x]dx= ….., where [x] denotes the greatest integer function
A10B8C6D4Area bounded by the relation [2x]+[y]=5, x,y > 0 is (where [⋅] represent greatest integer function)
A2B3C4D5
If f(x)=[2x], where [.] denotes the greatest integer function, then
View SolutionDraw the graph of [y]=sinx,x∈[0,2π] where [⋅] denotes the greatest integer function
View SolutionDraw the graph of [y]=sinx,x∈[0,2π] where [⋅] denotes the greatest integer function
View SolutionArea of the region bounded by [x]2=[y]2,ifx∈[1,5], where [ ] denotes the greatest integer function is:
View SolutionArea of the region bounded by [x]2=[y]2,ifx∈[1,5], where [ ] denotes the greatest integer function is:
View SolutionThe range of the function y=[x2]−[x]2 x∈[0,2] (where [] denotes the greatest integer function), is
View Solution
