Let f:R→R be a function defined by f(x)=max.{x,x3}. The set of all points where f(x) is NOT differenctiable is
(a) {−1,1}
(b) {−1,0}
(c ) {0,1}
(d) {−1,0,1}

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We have f(x)=max.{x,x3}
Draw the graphs of y=xandy=x3
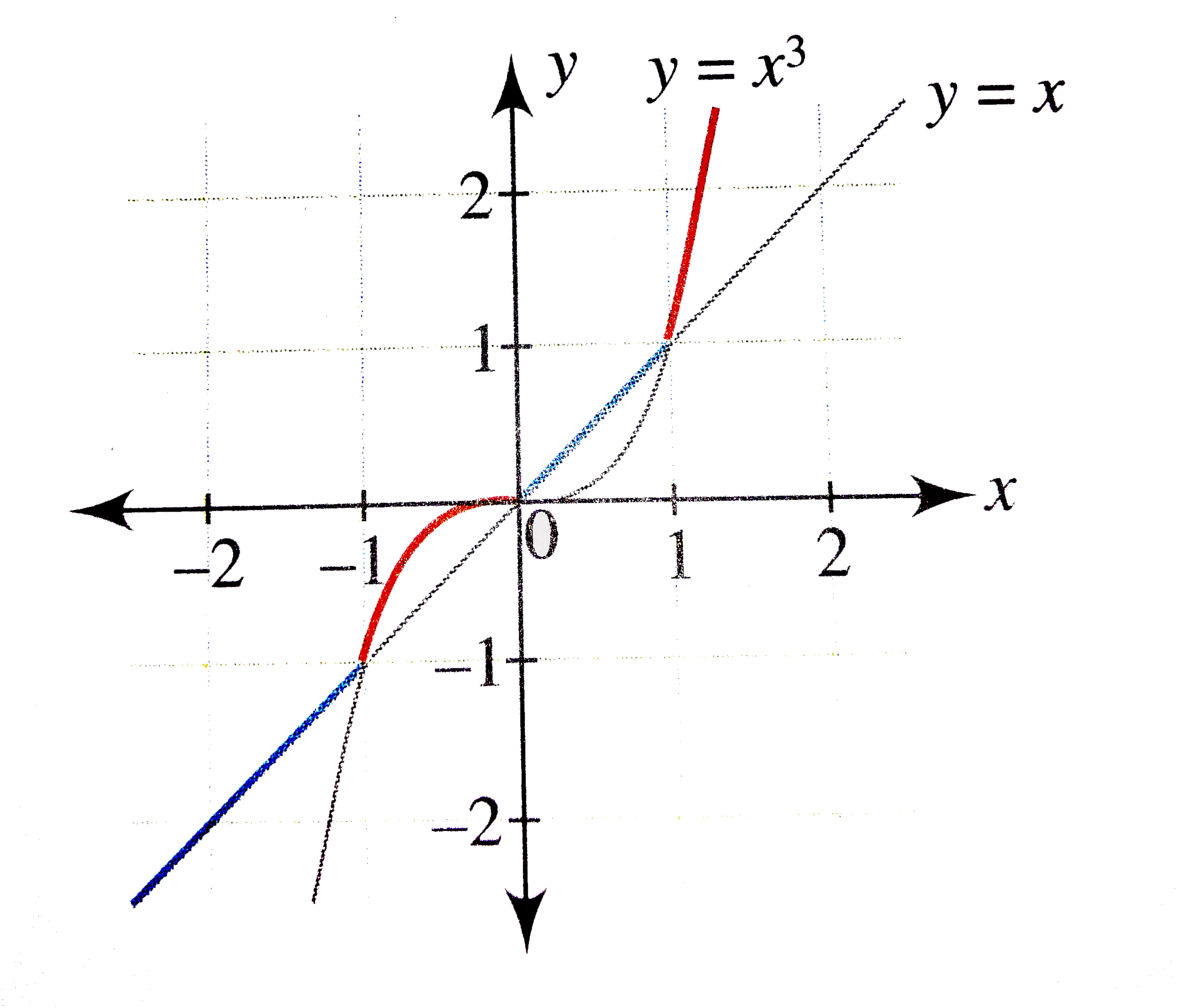
ocr_image
Graph of y=f(x) is combination of the combination of the blue and red-lined graphs.
From the graph, y=f(x) is non-differentiable at x=−1,x=0andx=1.

Updated on:21/07/2023
|
Class 12MATHSFUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Let f:R→R be a function defined by f(x)=max.{x,x3}. The set of all points where f(x) is NOT differenctiable is
    (a) {−1,1}
    (b) {−1,0}
    (c ) {0,1}
    (d) {−1,0,1}

    A{−1,1}
    B{−1,0}
    C{0,1}
    D{−1,0,1}

  • Let f:R→R be a function defined by f(x) = min {x+1,|x|+1}. Then which of the following is true.

    Af(x)≥1 for x∈R
    Bf(x) is not differentiable at x = 1
    Cf(x) is differentiable everywhere
    Df(x) is not differentiable at x = 0

  • Let f:R→R be a function defined byf(x)=min{x+1,|x|+1}. Then, which of the following is true?

    Af(x)>1for all x∈R
    Bf(x)is not differentiable at x=1
    Cf(x)is everywhere differentiable
    Df(x)is not differentiable at x=0