The eccentricity of the ellipse $9 x^{2} + 25 y^{2} - 18 x - 100 y - 116 = 0$ is $25 / 16$ b. $4 / 5$ c. $16 / 25$ d. $5 / 4$

Video Solution

Text Solution

Verified by Experts

We have $9 x^{2} + 25 y^{2} - 18 x - 100 y - 116 = 0$ .
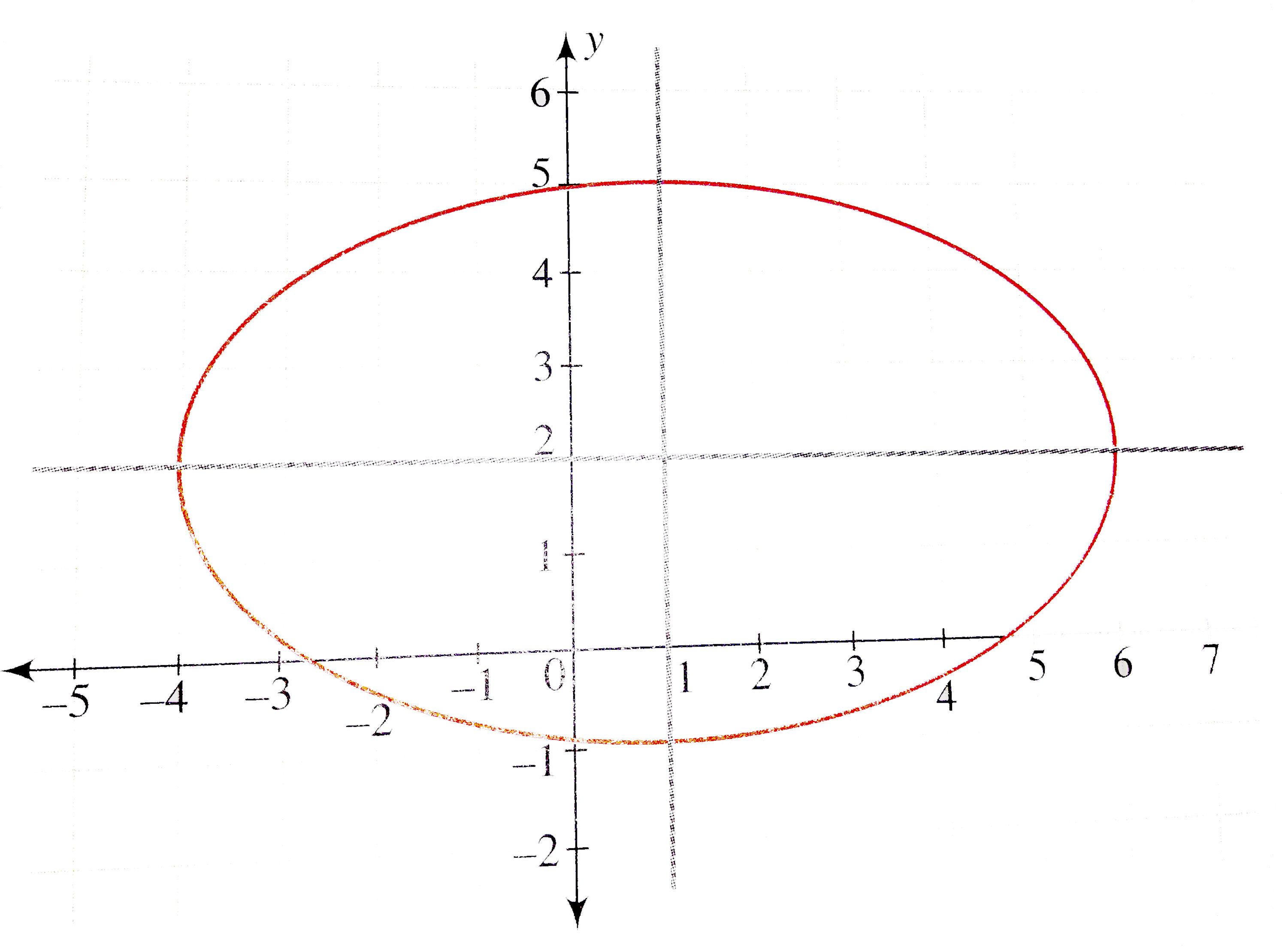
We can rewrite this as $\frac{{(x -)}^{2}}{25} + \frac{{(y - 2)}^{2}}{9} = 1$ .
Which is an ellipse having centre at (1, 2), foci at $(\pm 4, 2)$ .
Major axis $y = 2$ and minor axis as $x = 1$ .
The graph of the relation is as follows.

|

Updated on:21/07/2023

Class 12 MATHS FUNDAMENTAL OF MATHEMATICS

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
Eccentricity of the ellipse $\frac{x^{2}}{25} + \frac{y^{2}}{9} = 1$ is
A $\frac{4}{5}$
B $\frac{5}{4}$
C $\frac{3}{5}$
D $\frac{4}{9}$
Question 2 - Select One
The eccentricity of the ellipse $25 x^{2} + 16 y^{2} - 150 x - 175 = 0$ is
A $\frac{2}{5}$
B $\frac{2}{3}$
C $\frac{4}{5}$
D $\frac{3}{5}$
Question 3 - Select One
The eccentricity of the hyperbola $9 x^{2} - 16 y^{2} - 18 x - 64 y - 199 = 0$ is:
A $\frac{16}{9}$
B $\frac{5}{4}$
C $\frac{25}{16}$
Dzero

CENGAGE-GRAPHS OF ELEMENTARY FUNCTIONS -Exercise

Home
Ask Doubt
Profile