Question

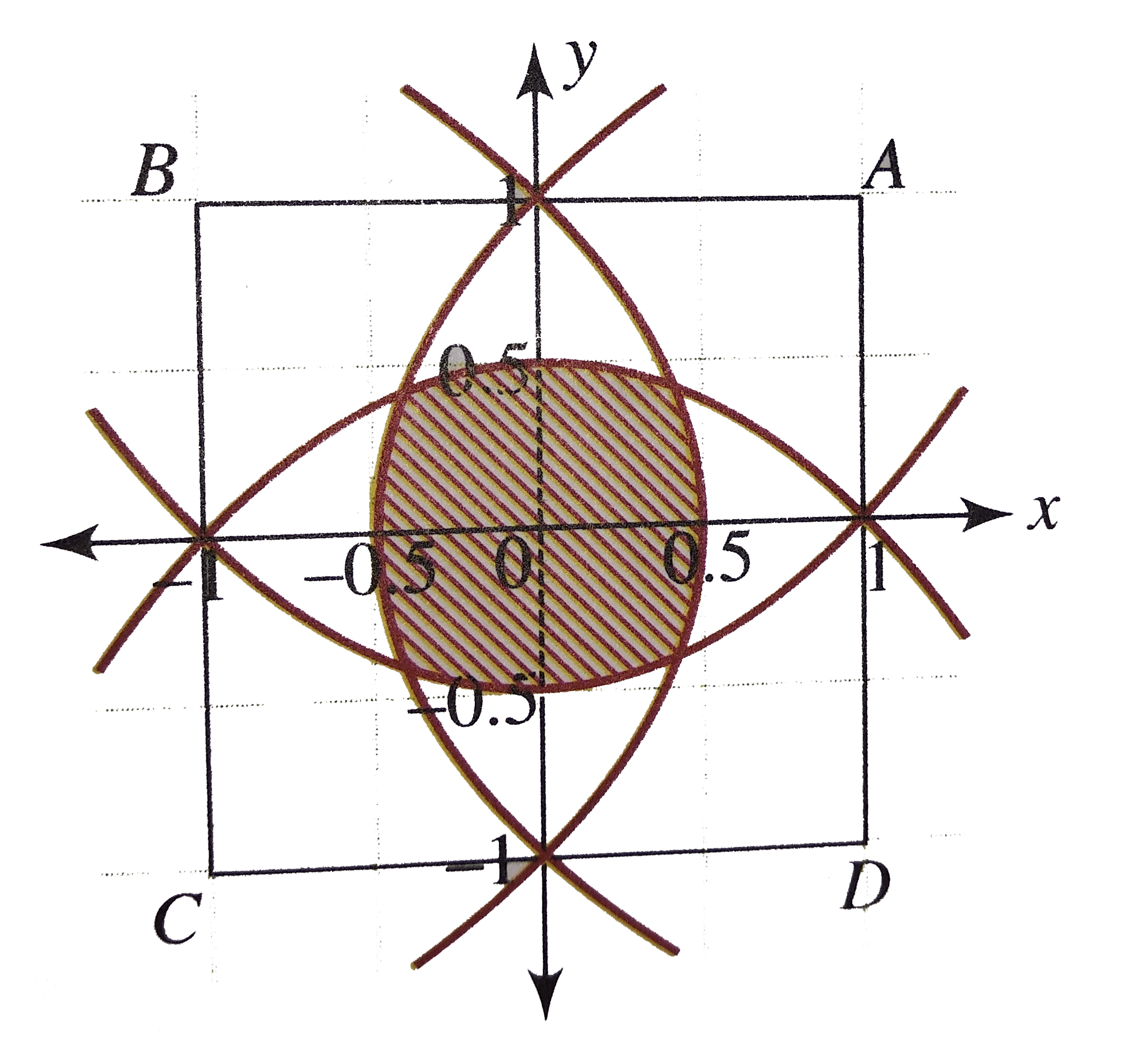
Consider a square with vertices at $(1,1),(-1,1),(-1,-1),and(1,-1)\stackrel{.}{}$
Set $S$
be the region consisting of all points inside the square which are nearer
to the origin than to any edge. Sketch the region $S$
and find its area.

Explanation

Let us consider any point `(x, y)` inside the square such that its distance from the origin `le` its distace from any of the edges, say AD.
`therefore " "OP lt PM`
`rArr" "sqrt((x^(2) +y^(2))) lt 1-x `
`rArr" "y^(2) le -2 (x- (1)/(2))" "`(i)
Above represents all points within and on the parabola `P_(1)`.
If we consider the edges BC, then `OP lt PN` will imply
`" "y^(2) le 2 (x+ (1)/(2))" "` (ii)
Similarly, if we consider the edges AB and CD, we will have
`" "x^(2) le -2(y -(1)/(2))" "`(iii)
`" " x^(2) le 2 (y + (1)/(2) ) " "`(iv)
Hence S consists of the region bounded by the four parabolas meeting the axes at `(pm (1)/(2), 0) and (0, pm (1)/(2))`.