Let M,N, P and Q be the mid points of the edges AB, CD, AC and BD respectively of the tetrahedron ABCD. Further, MN is perpendicular to both AB and CD and PQ is perpendicular to both AC and BD. Then which of the following is/are correct:
AB = CD
BC = DA
AC = BD
AN = BN
The correct Answer is:A, B, C, D
Step by step video, text & image solution for Let M,N, P and Q be the mid points of the edges AB, CD, AC and BD respectively of the tetrahedron ABCD. Further, MN is perpendicular to both AB and CD and PQ is perpendicular to both AC and BD. Then which of the following is/are correct: by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- VECTOR & 3DIMENSIONAL GEOMETRYBook:VK JAISWALChapter:VECTOR & 3DIMENSIONAL GEOMETRYExercise:Exercise-3 : Comprehension Type Problems
Explore 18 Videos
- VECTOR & 3DIMENSIONAL GEOMETRYBook:VK JAISWALChapter:VECTOR & 3DIMENSIONAL GEOMETRYExercise:Exercise-4 : Matching Type Problems
Explore 3 Videos
- VECTOR & 3DIMENSIONAL GEOMETRYBook:VK JAISWALChapter:VECTOR & 3DIMENSIONAL GEOMETRYExercise:Exercise-5 : Subjective Type Problems
Explore 16 Videos
- TRIGONOMETRIC EQUATIONS Book:VK JAISWALChapter:TRIGONOMETRIC EQUATIONS Exercise:Exercise-5 : Subjective Type Problems
Explore 9 Videos
Similar Questions
Knowledge Check
M and N are the mid-points of the diagonals AC and BD respectively of quadrilateral ABCD, then AB+AD+CB+CD is equal to
A2 MNB2NMC4 MND4 NMM and N are mid-point of the diagnols AC and BD respectivley of quadrilateral ABCD, then¯¯¯¯¯¯AB+¯¯¯¯¯¯AD+¯¯¯¯¯¯CB+¯¯¯¯¯¯CD=
A2¯¯¯¯¯¯¯¯MNB2¯¯¯¯¯¯¯¯NMC4¯¯¯¯¯¯¯¯MND4¯¯¯¯¯¯¯¯NMIn the given figure, M is the mid-point of both AC and BD. Then
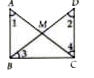 A∠1=∠2B∠1=∠4C∠2=∠4D∠1=∠3
A∠1=∠2B∠1=∠4C∠2=∠4D∠1=∠3
In a trapezium ABCD, if E and F be the mid-points of diagonal AC and BD respectively. Prove that EF=12(AB−CD).

View SolutionIn a □ABCD,AB∣∣DC. P and Q are the mid-points of ABandDC respectively AC,BD meet at O.Show that P,O,Q are collinear.
View SolutionIn a rectangle ABCD, E is the midpoint of AB, F is point on AC such that BF is perpendicular to AC and FE perpendicular to BD. Suppose BC=8√3. Find AB
View SolutionIn a parallelogram ABCD, E and F are the mid-points of sides AB and CD respectively. Show that the line segments AF and EC trisect the diagonal BD.

View SolutionIn a trapezium ABCD, AB is a parallel to CD. BD is perpendicular to AD. AC is perpendicular to BC. If AD=BC=15cmandAB=25cm, then the area of the trapezium is :
View Solution