Find the values of a for whch ${sin}^{\cdot} (- 1) x = | x - a |$ will have at least one solution.

Text Solution

Verified by Experts

(i) When $a < 0$
In this case, y = a-x must pass through $(1, \frac{π}{2})$
$∴ \frac{π}{2} = a - 1 \Rightarrow a = 1 + \frac{π}{2}$
(ii) When $a < 0$

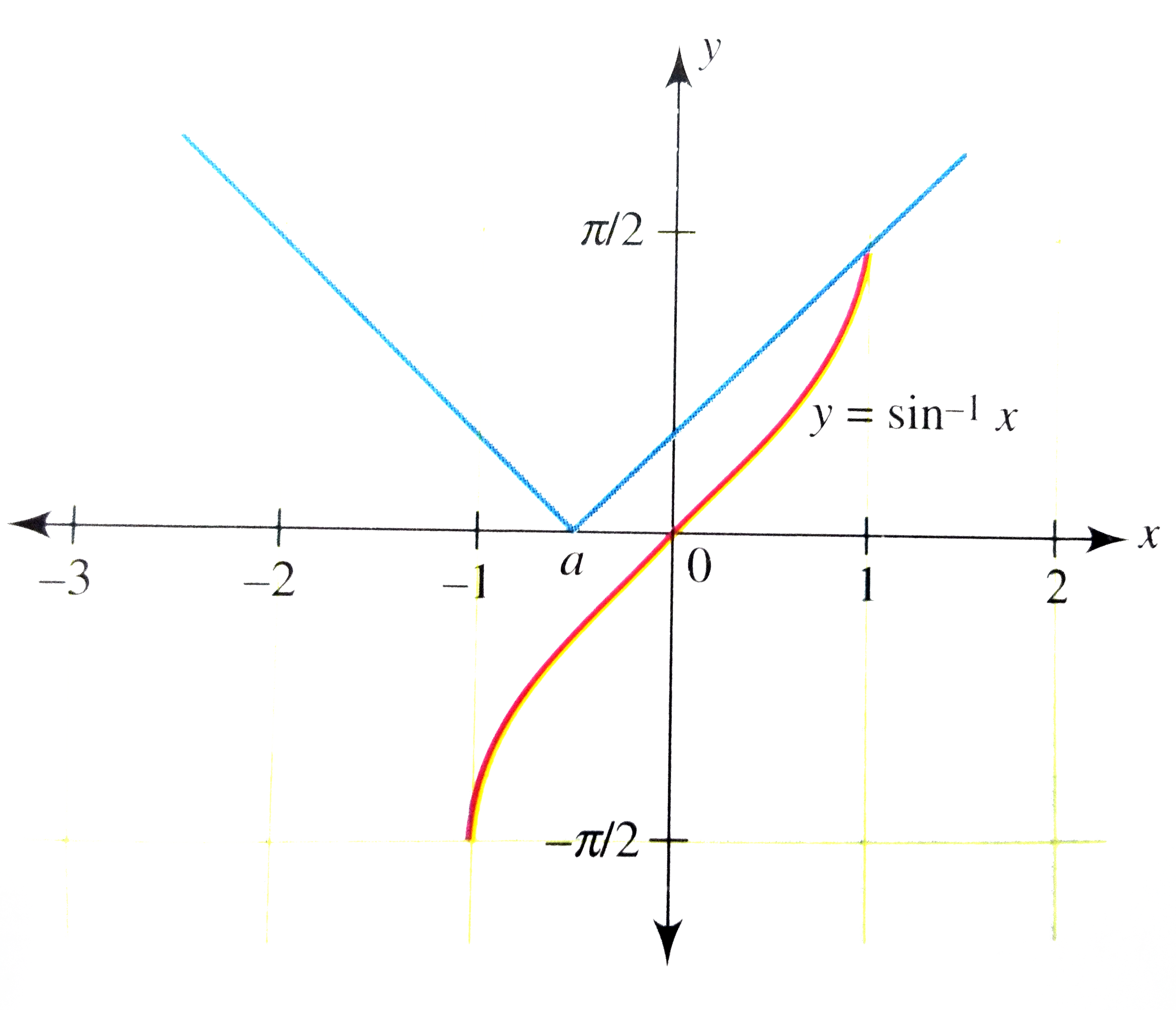
In this case,
$y = x - a must pass though (1, \frac{π}{2})$
$\frac{π}{2} = 1 - a$
$a = 1 - \frac{π}{2}$
For at least on solution.
$1 - \frac{π}{2} \leq a \leq 1 + \frac{π}{2}$

Updated on:21/07/2023

|

Class 12 MATHS INVERSE TRIGONOMETRIC FUNCTIONS

Topper's Solved these Questions

Similar Questions

CENGAGE-GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS-Exercise

Home
Ask Doubt
Profile