Drew the graph of $y = {cos}^{- 1} \sqrt{{log}_{[x]} (\frac{| x |}{x})}$ where $[\cdot]$ represents the greastest integer function.

Text Solution

Verified by Experts

We have $y = f (x) = {cos}^{- 1} \sqrt{{log}_{[x]} (\frac{| x |}{x})}$
$\frac{| x |}{x} = {\begin{matrix} 1 & x > 0 - 1 & x < 0 \end{matrix}$
We must have $x > 0$
Also $[x] > 0 and [x] \neq 1$
$∴ [x] \geq 2 or x \geq 2$
From (i) and (ii), the domain of the function is $(2, \infty)$
For $x \geq 2, \frac{| x |}{x} = 1$
$∴ {log}_{[x]} (\frac{| x |}{x}) = 0 - (for x \geq 2)$
$∴ \sqrt{{log}_{[x]} (\frac{| x |}{x})} = 0 (for x \geq 2)$
$∴ {cos}^{- 1} \sqrt{{log}_{[x]} (\frac{| x |}{x})} = \frac{π}{2}$
Hence, graph of $y = f (x) if the line y = \frac{π}{2} for x \in [2, \infty)$ .

Updated on:21/07/2023

|

Class 12 MATHS INVERSE TRIGONOMETRIC FUNCTIONS

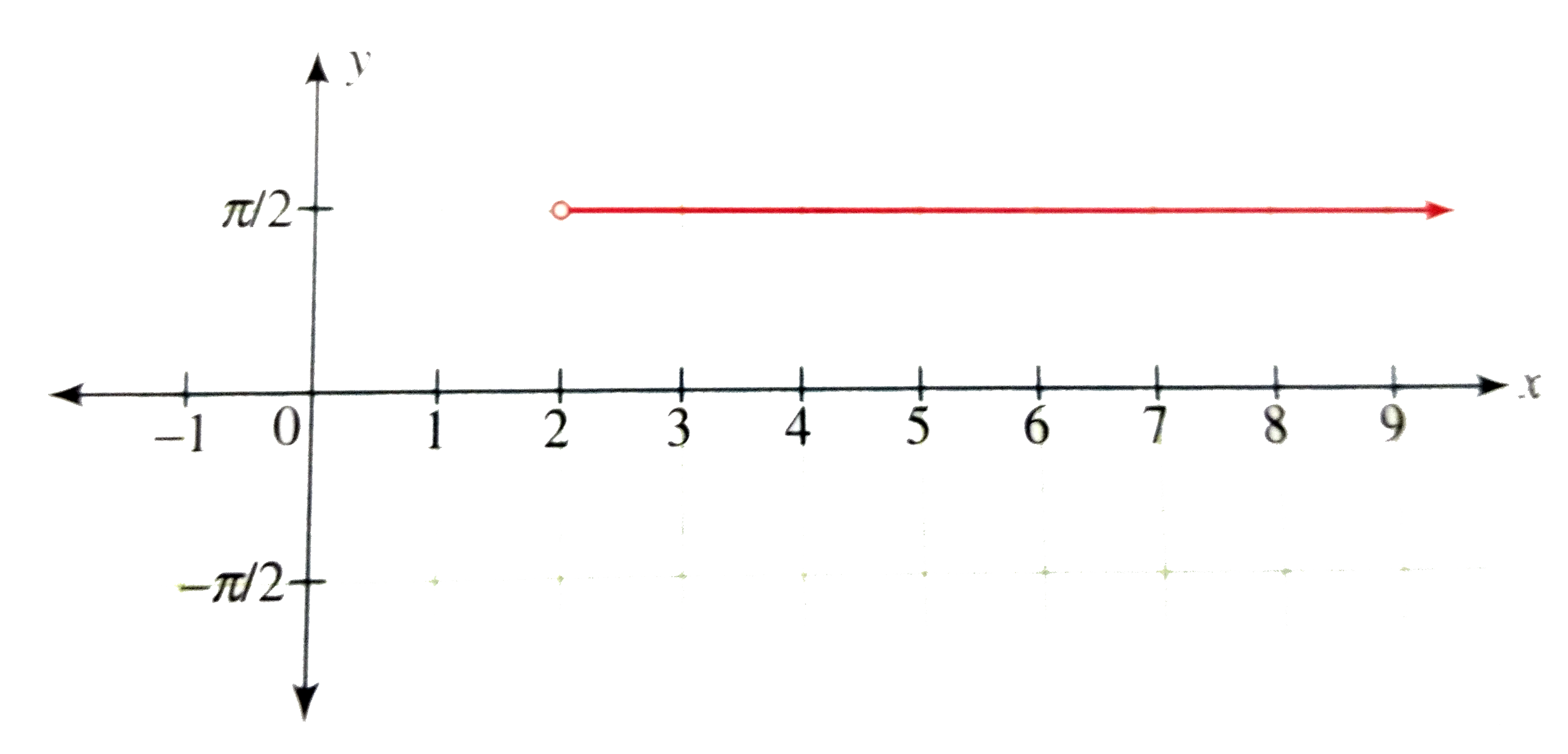
Topper's Solved these Questions

Similar Questions

Knowledge Check

The domain and range of $f (x) = {cos}^{- 1} \sqrt{{log}_{[x]} (\frac{| x |}{x})}$ where[.] denote the greatest integer function are respectively
A $[1, \infty), [0, π / 2]$
B $[2, \infty), [0, π / 2)$
C $[2, \infty), {π / 2}$
D $[1, \infty), {0}$

CENGAGE-GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS-Exercise

Home
Ask Doubt
Profile