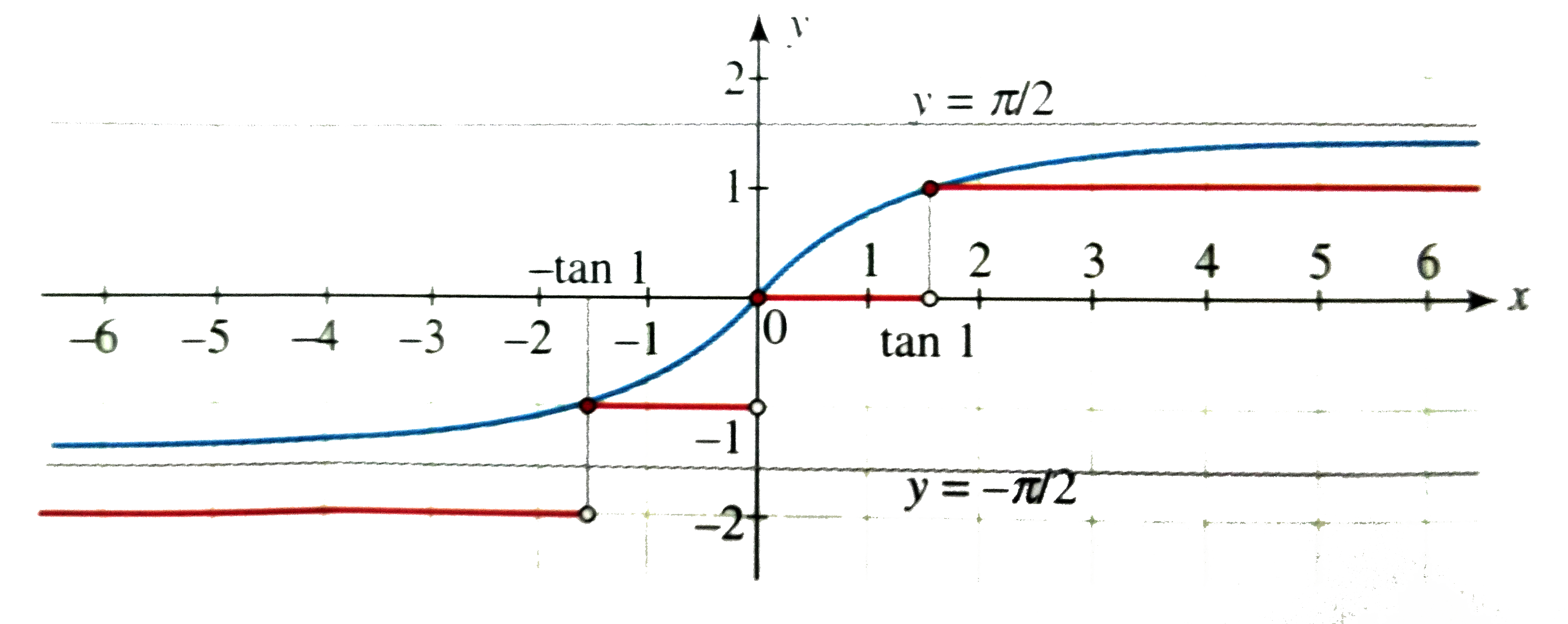
Draw the graph of f(x)=[tan−1x], where [⋅] represents the greatest integer function.
We have f(x)=[tan−1x]
Now−x/2≤tan−1x≤π/2 for x ∈R
∴ [tan−1x]=−2,−1,0,1
[tan−1x]=−2
∴ −π/2≤tn−1x≤−1
∴ −∞<−tan1
[tan−1x]=−1
∴ −tan≤tan−1x<0
−tan−11≤x<0
∴ 0≤tan−1x<1
∴ 0≤x<tan1
[tan−1x]=1
∴ 1≤tan−1x<π/2
∴ tan1≤x<∞
So the graph of f(x)=[tan−1x] can be drawn as shwon in the following figure.
Topper's Solved these Questions
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGECHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - Exercise
18 Videos
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
22 Videos
Similar Questions
Draw the graph of f(x)=[cot−1x], where [⋅] represents the greatest integer funtion.
View SolutionDraw the graph of f(x)=[cot−1x], where [⋅] represents the greatest integer funtion.
View SolutionDraw the graph of f(x)=cosπ[x], where [⋅] represents the greatest integer function. Find the period of the function.
View SolutionDraw the graph of f(x)=cosπ[x], where [⋅] represents the greatest integer function. Find the period of the function.
View SolutionDraw the graph of y=[4−x2],|x|≤2, where [.] represents the greatest integer function.
View SolutionDraw the graph of y=[4−x2],|x|≤2, where [.] represents the greatest integer function.
View SolutionDraw a graph of f(x)=sin{x}, where {x} represents the greatest integer function.
View SolutionDraw a graph of f(x)=sin{x}, where {x} represents the greatest integer function.
View SolutionDraw the graph of f(x)=2x2[x] where [.] represents greatest integer function and find the domain and range.
View SolutionDraw the graph of f(x)=2x2[x] where [.] represents greatest integer function and find the domain and range.
View Solution
